道格拉斯-普克算法(Douglas–Peucker algorithm,亦称为拉默-道格拉斯-普克算法、叠代适应点算法、分裂与合併算法)是将曲线近似表示为一系列点,并减少点的数量的一种算法。它的优点是具有平移和旋转不变性,给定曲线与阈值后,抽样结果一定。
基本介绍
- 中文名:道格拉斯-普克算法
- 外文名:Douglas–Peucker algorithm
- 亦称为:拉默-道格拉斯-普克算法
- 提出:1973年
简要说明
道格拉斯-普克算法(Douglas–Peucker algorithm,亦称为拉默-道格拉斯-普克算法、叠代适应点算法、分裂与合併算法)是将曲线近似表示为一系列点,并减少点的数量的一种算法。该算法的原始类型分别由乌尔斯·拉默(Urs Ramer)于1972年以及大卫·道格拉斯(David Douglas)和托马斯·普克(Thomas Peucker)于1973年提出,并在之后的数十年中由其他学者予以完善。
算法的基本思路是:对每一条曲线的首末点虚连一条直线,求所有点与直线的距离,并找出最大距离值dmax ,用dmax与限差D相比:若dmax <D,这条曲线上的中间点全部捨去;若dmax ≥D,保留dmax 对应的坐标点,并以该点为界,把曲线分为两部分,对这两部分重複使用该方法。
详细步骤
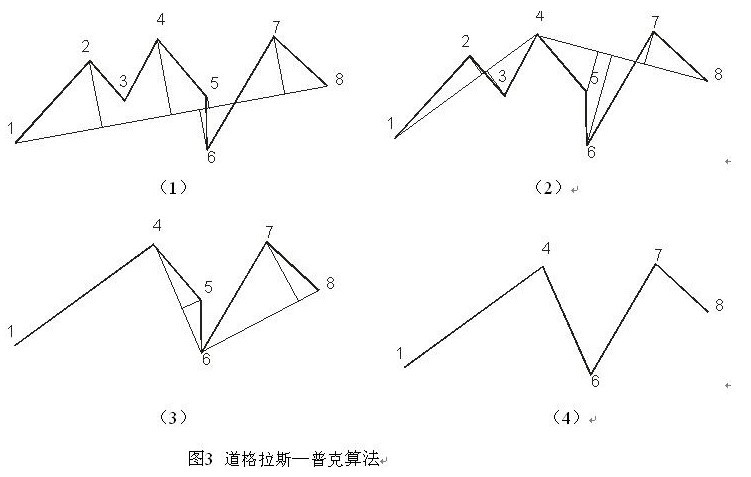
(1) 在曲线首尾两点间虚连一条直线,求出其余各点到该直线的距离,如右图(1)。
(2)选其最大者与阈值相比较,若大于阈值,则离该直线距离最大的点保留,否则将直线两端点间各点全部捨去,如右图(2),第4点保留。
(3)依据所保留的点,将已知曲线分成两部分处理,重複第1、2步操作,叠代操作,即仍选距离最大者与阈值比较,依次取捨,直到无点可捨去,最后得到满足给定精度限差的曲线点坐标,如图(3)、(4)依次保留第6点、第7点,捨去其他点,即完成线的化简。
实现代码
packagecom.mapbar.jts;/***ClassPoint.java*/publicclassPoint{ /***点的X坐标*/ privatedoublex = 0; /***点的Y坐标*/ privatedoubley = 0; /***点所属的曲线的索引*/ privateintindex = 0; publicdoublegetX() { returnx; } publicvoidsetX(doublex) { this.x = x; } publicdoublegetY() { returny; } publicvoidsetY(doubley) { this.y = y; } publicintgetIndex() { returnindex; } publicvoidsetIndex(intindex) { this.index = index; } /***点数据的构造方法* *@param x *点的X坐标 *@param y *点的Y坐标 *@param index点所属的曲线的索引 */ publicPoint(doublex, doubley, intindex){ this.x = x; this.y = y; this.index = index; }}packagecom.mapbar.jts;importjava.util.ArrayList;importjava.util.List;importcom.vividsolutions.jts.geom.Coordinate;importcom.vividsolutions.jts.geom.Geometry;importcom.vividsolutions.jts.io.ParseException;importcom.vividsolutions.jts.io.WKTReader;/***ClassDouglas.java*/publicclassDouglas{ /***存储採样点数据的鍊表*/ publicList < Point > points = newArrayList < Point > (); /***控制数据压缩精度的极差*/ privatestaticfinaldoubleD = 1; privateWKTReaderreader; /***构造Geometry**@paramstr*@return*/ publicGeometrybuildGeo(Stringstr) { try { if (reader == null) { reader = newWKTReader(); } returnreader.read(str); } catch(ParseExceptione) { thrownewRuntimeException("buildGeometryError", e); } } /***读取採样点*/ publicvoidreadPoint() { Geometryg = buildGeo("LINESTRING(14,23,42,66,77,86,95,1010)"); Coordinate[] coords = g.getCoordinates(); for (inti = 0; i < coords.length; i++) { Pointp = newPoint(coords[i].x, coords[i].y, i); points.add(p); } } /***对矢量曲线进行压缩**@paramfrom*曲线的起始点*@paramto*曲线的终止点*/ publicvoidcompress(Pointfrom, Pointto) { /***压缩算法的开关量*/ booleanswitchvalue = false; /***由起始点和终止点构成的直线方程一般式的係数*/ System.out.println(from.getY()); System.out.println(to.getY()); doubleA = (from.getY() - to.getY()) / Math.sqrt(Math.pow((from.getY() - to.getY()), 2) + Math.pow((from.getX() - to.getX()), 2)); /***由起始点和终止点构成的直线方程一般式的係数*/ doubleB = (to.getX() - from.getX()) / Math.sqrt(Math.pow((from.getY() - to.getY()), 2) + Math.pow((from.getX() - to.getX()), 2)); /***由起始点和终止点构成的直线方程一般式的係数*/ doubleC = (from.getX() * to.getY() - to.getX() * from.getY()) / Math.sqrt(Math.pow((from.getY() - to.getY()), 2) + Math.pow((from.getX() - to.getX()), 2)); doubled = 0; doubledmax = 0; intm = points.indexOf(from); intn = points.indexOf(to); if (n == m + 1) return; Pointmiddle = null; List < Double > distance = newArrayList < Double > (); for (inti = m + 1; i < n; ++) { d = Math.abs(A * (points.get(i).getX()) + B * (points.get(i).getY()) + C) / Math.sqrt(Math.pow(A, 2) + Math.pow(B, 2)); distance.add(d); } dmax = distance.get(0); for (intj = 1; j < distance.size(); j++) { if (distance.get(j) > dmax) dmax = distance.get(j); } if (dmax > D) switchvalue = true; else switchvalue = false; if (!switchvalue) { //删除Points(m,n)内的坐标 for (inti = m + 1; i < n; i++) points.get(i).setIndex( - 1); } else { for (inti = m + 1; i < n; i++) { if ((Math.abs(A * (points.get(i).getX()) + B * (points.get(i).getY()) + C) / Math.sqrt(Math.pow(A, 2) + Math.pow(B, 2)) == dmax)) middle = points.get(i); } compress(from, middle); compress(middle, to); } } publicstaticvoidmain(String[] args) { Douglasd = newDouglas(); d.readPoint(); d.compress(d.points.get(0), d.points.get(d.points.size() - 1)); for (inti = 0; i < d.points.size(); i++) { Pointp = d.points.get(i); if (p.getIndex() > -1) { System.out.print(p.getX() + "" + p.getY() + ","); } } }}