非线性系统：一个系统,如果其输出不与其输入成正比，则它是非线性的。从数学上看，非线性系统的特徵是叠加原理不再成立。叠加原理是指描述系统的方程的两个解之和仍为其解。叠加原理可以通过两种方式失效。其一，方程本身是非线性的。其二,方程本身虽然是线性的,但边界是未知的或运动的。

“线性”与“非线性”是两个数学名词。所谓“线性”是指两个量之间所存在的正比关係。若在直角坐标系上画出来，则是一条直线。由线性函式关係描述的系统叫线性系统。线上性系统中，部分之和等于整体。描述线性系统的方程遵从叠加原理，即方程的不同解加起来仍然是原方程的解。这是线性系统最本质的特徵之一。“非线性”是指两个量之间的关係不是“直线”关係，在直角坐标系中呈一条曲线。最简单的非线性函式是一元二次方程即抛物线方程。简单地说，一切不是一次的函式关係，如一切高于一次方的多项式函式关係，都是非线性的。由非线性函式关係描述的系统称为非线性系统。

定性地说，线性关係只有一种，而非线性关係则千变万化，不胜枚举。线性是非线性的特例，它是简单的比例关係，各部分的贡献是相互独立的；而非线性是对这种简单关係的偏离，各部分之间彼此影响，发生耦合作用，这是产生非线性问题的複杂性和多样性的根本原因。正因为如此，非线性系统中各种因素的独立性就丧失了：整体不等于部分之和，叠加原理失效，非线性方程的两个解之和不再是原方程的解。因此，对于非线性问题只能具体问题具体分析。

线性与非线性现象的区别一般还有以下特徵：

（1）在运动形式上，线性现象一般表现为时空中的平滑运动，并可用性能良好的函式关係表示，而非线性现象则表现为从规则运动向不规则运动的转化和跃变；

（2）线性系统对外界影响的回响平缓、光滑，而非线性系统中参数的极微小变动，在一些关节点上，可以引起系统运动形式的定性改变。在自然界和人类社会中大量存在的相互作用都是非线性的，线性作用只不过是非线性作用在一定条件下的近似。

多变数系统（multivariable systems）是指具有多个输入量或输出量的系统，又称多输入多输出系统。

同单变数系统相比，多变数系统的控制複杂得多。在多变数控制系统中，被控对象、测量元件、控制器和执行元件都可能具有一个以上的输入变数或一个以上的输出变数。例如汽轮机的蒸汽压力和转速控制，石油化工生产中精馏塔的塔顶温度和塔底温度控制，涡轮螺旋桨发动机转速和涡轮进气温度的控制等，都是多变数系统的控制问题。多变数系统不同于单变数系统，它的每个输出量通常都同时受到几个输入量的控制和影响，这种现象称为耦合或交叉影响。交叉影响的存在使多变数系统很可能成为一种条件稳定系统。例如，在调试或运行过程中若增益发生变化或某一元件（例如感测器）断开或失灵，就可能导致不稳定。这是多变数系统特有的问题。在多变数控制系统的设计中，对于交叉影响的处理，常採用两种方式：①通过引入适当的附加控制器，实现一个输入只控制一个输出，称为解耦控制（见解耦控制问题）；②协调各个输入和输出间的关係，使耦合的存在有利于改善系统的控制性能，称为协调控制。此外，也可採用其他形式的指标来设计多变数系统的控制器。（见线性系统理论）

1)集中控制便于维护

2)由表头到单表头降低数据误差

多变数系统的结构特点如图所示：

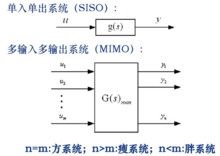
多变数非线性系统（Multivariable nonlinear systems）是指既具有多变数系统的特徵，又具有非线性系统的特徵，即状态变数和输出变数相对于输入变数的运动特性不能用线性关係描述，同时具有多个输入量或输出量的控制系统。

线性因果关係的基本属性是满足叠加原理（见线性系统）。在非线性控制系统中必定存在非线性元件，但逆命题不一定成立。描述非线性系统的数学模型，按变数是连续的或是离散的，分别为非线性微分方程组或非线性差分方程组。

非线性控制系统的形成基于两类原因，一是被控系统中包含有不能忽略的非线性因素，二是为提高控制性能或简化控制系统结构而人为地採用非线性元件。

对于非线性系统，建立数学模型的问题要比线性系统困难得多，至于解非线性微分方程，用其解来分析非线性系统的性能，就更加困难了。这是因为除了极特殊的情况外，多数非线性微分方程无法直接求得解析解。所以到目前为止，还没有一个成熟、通用的方法可以用来分析和设计各种不同的非线性系统，目前研究非线性系统常用的工程近似方法有：

相平面法是时域分析法在非线性系统中的推广套用，通过在相平面上绘製相轨迹，可以求出微分方程在任何初始条件下的解，所得结果比较精确和全面。但对于高于二阶的系统，需要讨论变数空间中的曲面结构，从而大大增加了工程使用的难度。故相平面法仅适用于一、二阶非线性系统的分析。

描述函式法是一种[5]频域的分析方法，它是线性理论中的频率法在非线性系统中的推广套用，其实质是套用谐波线性化的方法，将非线性元件的特性线性化，然后用频率法的一些结论来研究非线性系统。这种方法不受系统阶次的限制，且所得结果也比较符合实际，故得到了广泛套用。

用模拟计算机或数字计算机直接求解非线性微分方程，对于分析和设计複杂的非线性系统，几乎是唯一有效的方法。随着计算机的广泛套用，这种方法定会有更大的发展。

应当指出，这些方法主要是解决非线性系统的“分析”问题，而且是以稳定性问题为中心展开的，非线性系统“综合”方法的研究远不如稳定性问题的成果，可以说到目前为止还没有一种简单而实用的综合方法，可以用来设计任意的非线性控制系统。

七十年代以后，非线性控制得到比较大的发展，并呈现出多方向发展的趋势，可归纳为以下三大方面:

在各种特定非线性模型中，以Hammerstein模型和双线性模型所代表的系统研究得较多.利用这些模型，可以描述众多的非线性系统，再与一些先进的控制算法相结合以构成非线性控制系统.从目前的研究情况来说，以这些特定模型为基础构成非线性控制系统的主要算法有:自适应控制、预测控制、内模控制等。这方面目前仍处于发展态势：一方面各种新的非线性模型尚有推出，同时以这些模型为基础的先进算法也在发展;另外，从原来的单变数非线性系统拓展到多变数非线性系统.这些非线性控制方法的特点是比较实用且简单。

八十年代初出现的用微分几何、微分代数方法来研究非线性系统是非线性系统研究的一大突破.通过变换，非线性系统可以化为线性系统那样来处理.这种变换不同于经典时期的在某点附近的近似线性化，而是在大範围(甚至全局的)的精确线性化.运用这些方法，有可能实现非线性系统的大範围分析综合。由于这些原因，使得这一领域的研究成为目前控制界的热门研究课题之一。基于微分几何的非线性控制方法对于一般的非线性系统尚无能为力。另外，此方法需要有精确的数学模型，这在实际套用中亦受到很大的限制。

近年来发展迅速的人工神经网路、模糊控制等，由于其自身的非线性特性，使其在本质上既可用于线性控制，亦可套用于非线性控制.特别是人工神经网路，经训练可以逼近任意非线性函式，这就使其在非线性控制中大有作为。基于神经网路的预测控制、自适应控制、内模控制、逆模型控制等，都在一定程度上获得了较好的非线性控制效果。还有智慧型控制中的交叉综合方法亦可套用于非线性控制，如模糊神经网路控制等。这方面亦是控制界的一大热点.人们尚在不断地研究适用于一般非线性系统的有效且实用的控制策略。