1928年，R．V．L．哈特莱提出了信息定量化的初步构想，他将符号取值数m的对数定义为信息量，即I=log₂m。对信息量作深入、系统研究的是资讯理论创始人C．E．仙农。1948年，仙农指出信源给出的符号是随机的，信源的信息量应是机率的函式，以信源的信息熵表示，即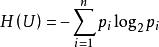 ，其中P_i表示信源不同种类符号的机率，i= 1，2，…，n。

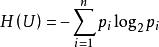
例如，若一个连续信源被等机率量化为4层，即4 种符号。这个信源每个符号所给出的信息最应为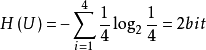 ，与哈特莱公式I=log₂m=log₂4=2bit一致。实质上哈特莱公式是等机率时仙农公式的特例。

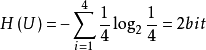
基本内容 实际信源多为有记忆序列信源，只有在掌握全部序列的机率特性后，才能计算出该信源中平均一个符号的熵H_L（U）（L为符号数这通常是困难的。如果序列信源简化为简单的一阶、齐次、遍历马氏链，则比较简单。根据符号的条件机率P_ji（即前一符号为i条件下后一符号为j的机率），可以求出遍历信源的稳定机率P_i，再由P_i和P_ji求出H_L（U）。即如图1 。

图1

其中H（U|V）称为条件熵，即前一符号V已知时后一符号U的不确定度。

信息量与信息熵在概念上是有区别的。在收到符号之前是不能肯定信源到底传送什幺符号，通信的目的就是使接收者在收到符号后，解除对信源存在的疑义（不确定度），使不确定度变为零。这说明接收者从传送者的信源中获得的信息量是一个相对的量（H（U）-0）。而信息熵是描述信源本身统计特性的物理量，它表示信源产生符号的平均不确定度，不管有无接收者，它总是客观存在的量。

从信源中一个符号V中获取另一符号u的信息

量可用互信息表示，即

I（U；V）= H（U）-H（U|V）

表示在收到V以后仍然存在对信源符号U的疑义（不确定度）。一般情况下

I（U；V）≤H（U）

即获得的信息量比信源给出的信息熵要小。

连续信源可有无限个取值，输出信息量是无限大，但互信息是两个熵值之差，是相对量。这样，不论连续或离散信源，接收者获取的信息量仍然保持信息的一切特性，且是有限值。

信息量的引入，使通信、信息以及相关学科得以建立在定量分析的基础上，为各有关理论的确立与发展提供了保证。

所谓信息量是指从N个相等可能事件中选出一个事件所需要的信息度量或含量，也就是在辩识N个事件中特定的一个事件的过程中所需要提问"是或否"的最少次数.

香农（C. E. Shannon）资讯理论套用机率来描述不确定性。信息是用不确定性的量度定义的.一个讯息的可能性愈小，其信息愈多；而讯息的可能性愈大，则其信息愈少.事件出现的机率小，不确定性越多，信息量就大，反之则少。

信息现代定义。[2006年，医学信息（杂誌），邓宇等].

信息是物质、能量、信息及其属性的标示。逆维纳信息定义

信息是确定性的增加。逆香农信息定义

信息是事物现象及其属性标识的集合。2002年

在数学上，所传输的讯息是其出现机率的单调下降函式。如从64个数中选定某一个数，提问：“是否大于32?”，则不论回答是与否，都消去了半数的可能事件，如此下去，只要问6次这类问题，就可以从64个数中选定一个数。我们可以用二进制的6个位来记录这一过程，就可以得到这条信息。

信息多少的量度。1928年R.V.L.哈特莱首先提出信息定量化的初步构想，他将讯息数的对数定义为信息量。若信源有m种讯息，且每个讯息是以相等可能产生的，则该信源的信息量可表示为I=logm。但对信息量作深入而系统研究，还是从1948年C.E.香农的奠基性工作开始的。

信息的统计特徵描述是早在1948年香农把热力学中熵的概念与熵增原理引入信息理论的结果。先行考察熵增原理。热力学中的熵增原理是这样表述的：存在一个态函式－熵，只有不可逆过程才能使孤立系统的熵增加，而可逆过程不会改变孤立系统的熵。从中可以看出：一、熵及熵增是系统行为；二、这个系统是孤立系统；三、熵是统计性状态量，熵增是统计性过程量。讨论信息的熵表述时，应充分注意这些特徵的存在。并且知道，给定系统中发生的信息传播，是不可逆过程。

在资讯理论中，认为信源输出的讯息是随机的。即在未收到讯息之前，是不能肯定信源到底传送什幺样的讯息。而通信的目的也就是要使接收者在接收到讯息后，儘可能多的解除接收者对信源所存在的疑义（不定度），因此这个被解除的不定度实际上就是在通信中所要传送的信息量。因此，接收的信息量在无干扰时，在数值上就等于信源的信息熵，式中P(xi）为信源取第i个符号的机率。但在概念上，信息熵与信息量是有区别的。信息熵是描述信源本身统计特性的一个物理量。它是信源平均不定度，是信源统计特性的一个客观表征量。不管是否有接收者它总是客观存在的。信息量则往往是针对接收者而言的，所谓接收者获得了信息，是指接收者收到讯息后解除了对信源的平均不定度，它具有相对性。对于信息量的说明须引入互信息的概念。

E.H.Weber

在资讯理论中，互信息的定义是：I(X；Y)=H(X）－H(X|Y），数式右边后一项称为条件熵，对离散讯息可表示，它表示已知Y以后，对X仍存在的不定度。因此，互信息I(X;Y）是表示当收到Y以后所获得关于信源X的信息量。与互信息相对应，常称H(X)为自信息。互信息具有三个基本性质。

公式

①非负性：I(X;Y）≥0，仅当收到的讯息与传送的讯息统计独立时，互信息才为0。

②互信息不大于信源的熵：I(X;Y）≤H(X），即接收者从信源中所获得的信息必不大于信源本身的熵。仅当信道无噪声时，两者才相等。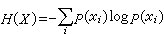

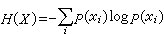公式

③对称性：I(X;Y)=I(Y;X），即Y隐含X和X隐含Y 的互信息是相等的。

对于连续信源的互信息，它仍表示两个熵的差值，所以也可直接从离散情况加以推广，并保持上述离散情况的一切特性，即 实际信源是单个讯息信源的组合，所以实际信源的互信息I(X;Y）也可以直接从上述单个讯息的互信息I(X；Y）加以推广，即I(X;Y)=H(X)-H(X│Y）。配图相关连线

资讯理论创始人C.E.Shannon，1938年首次使用比特（bit）概念：1（bit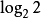）= 。它相当于对二个可能结局所作的一次选择量。资讯理论採用对随机分布机率取对数的办法，解决了不定度的度量问题。

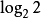
m个对象集合中的第i个对象，按n个观控指标测度的状态集合的

全信息量TI= 。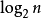

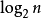
从试验后的结局得知试验前的不定度的减少，就是申农界定的信息量，即

自由信息量FI=－∑pi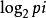 ，（i=1,2，…，n）。

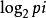
式中pi是与随机变数xi对应的观控权重，它趋近映射其实际状态的分布机率。由其内在分布构成引起的在试验前的不定度的减少，称为先验信息或谓约束信息量。风险是潜藏在随机变数尚未变之前的内在结构能（即形成该种结构的诸多作用中还在继续起作用的有效能量）中的。可以显示、映射这种作用的是

约束信息量BI=TI-FI。

研究表明，m个观控对象、按n个观控指标进行规範化控制的比较收益优选序，与其自由信息量FI之优选序趋近一致；而且各观控对象“愈自由，风险愈小”；约束信息量BI就是映射其风险的本徵性测度，即风险熵。

把信息描述为信息熵，是状态量，其存在是绝对的；信息量是熵增，是过程量，是与信息传播行为有关的量，其存在是相对的。在考虑到系统性、统计性的基础上，认为：信息量是因具体信源和具体信宿範围决定的，描述信息潜在可能流动价值的统计量。本说法符合熵增原理所要求的条件：

一、“具体信源和信宿範围”构成孤立系统，信息量是系统行为而不仅仅是信源或信宿的单独行为。

二、界定了信息量是统计量。此种表述还说明，信息量并不依赖具体的传播行为而存在，是对“具体信源和具体信宿”的某信息潜在可能流动价值的评价，而不是针对已经实现了的信息流动的。由此，信息量实现了信息的度量。

如何计算信息量的多少？在日常生活中，极少发生的事件一旦发生是容易引起人们关注的，而司空见惯的事不会引起注意，也就是说，极少见的事件所带来的信息量多。如果用统计学的术语来描述，就是出现机率小的事件信息量多。因此，事件出现得机率越小，信息量愈大。即信息量的多少是与事件发生频繁（即机率大小）成反比。

⒈如已知事件Xi已发生，则表示Xi所含有或所提供的信息量

H(Xi) = −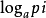

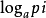
例题：若估计在一次西洋棋比赛中谢军获得冠军的可能性为0.1（记为事件A），而在另一次西洋棋比赛中她得到冠军的可能性为0.9（记为事件B）。试分别计算当你得知她获得冠军时，从这两个事件中获得的信息量各为多少？

H(A)=-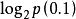 ≈3.32（比特）

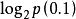
H(B)=-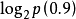 ≈0.152（比特）

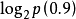
⒉统计信息量的计算公式为：

Xi —— 表示第i个状态（总共有n种状态）；

P(Xi）——表示第i个状态出现的机率；

H(X）——表示用以消除这个事物的不确定性所需要的信息量。

例题：向空中投掷硬币，落地后有两种可能的状态，一个是正面朝上，另一个是反面朝上，每个状态出现的机率为1/2。如投掷均匀的正六面体的骰子，则可能会出现的状态有6个，每一个状态出现的机率均为1/6。试通过计算来比较状态的不肯定性与硬币状态的不肯定性的大小。

H（硬币）= -（2×1/2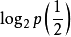）× ≈1（比特）

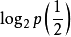
H（骰子）= -（1/6×6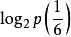）× ≈2.6（比特）

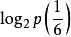
由以上计算可以得出两个推论：

[推论1] 若且唯若某个P(Xi)=1，其余的都等于0时， H(X)= 0。

[推论2]若且唯若某个P(Xi)=1/n，i=1， 2，……， n时，H(X）有极大值log n。

如今被称为信息化社会，现代情报学理论及其套用，非常注重信息量化测度。1980年代，英国着名情报学家B.C.布鲁克斯，在阐述人之信息（情报）获取过程时，深入研究了感觉信息的接收过程，并将透视原理──对象的观察长度Z与从观察者到被观察对象之间的物理距离X成反比，引入情报学，提出了Z=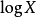 的对数假说。用此能较好地说明信息传递中，情报随时间、空间、学科（行业）的不同而呈现的对数变换。然而，关于用户的情报搜寻行为，在其信息来源上，“获取距离最近的比例最高，最远的比例最低”的结论，在跨域一体、存在国际网际网路，需要有新的理论进行新的概括。对数透视变换，源于实验心理物理学。1846年德国心理学家E.H.Weber提出了韦伯公式：△I/I=k。这里，△I代表刚可感觉到的差别阈限，I代表标準刺激物理量，k是小于1的常数。后来，Fechner把这个关于差别阈限的规律称之为韦伯定律，并于1860年在此基础上提出了着名的费肯纳对数定律：心理的感觉量值S是物理刺激量I的对数函式，即S=cLogI，c是由特殊感觉方式确定的常数。

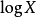
1957年Stevens提出幂定律：S=bIa，a与b为特徵常数。心理物理函式究竟是服从幂定律还是服从对数定律？W.S.Togerson认为，这不能通过实验解决，而是一个在实验中进行选择的问题。G.Ekman在假定Fechner的对数定律是普遍正确的前提下，推导出幂定律是对数定律的一个特例。

中国有突出贡献的科学家程世权，在1990年出版的《模糊决策分析》一书中，评介引述于宏义等对“系统的定性和定量转化，总结归纳出了一种方便可行、科学可靠的定性排序与定量转化的方法”。于宏义等之方法，在利用显在的频数信息的同时，巧妙利用了潜在的泛序信息——权数，使模糊系统简便有效地转化成明晰的工程系统。其测度模式是：

F(I)=Ln(max{I}-I+2）/Ln(max{I}+1）。

式中，I为所论对象按一定指标的排序序号，F(I）为其隶属度。实际套用中巧妙运用“自动连锁”机制，确实简便、实用、有效。所谓“自动连锁”机制，就是“评价者在评价他人他事他物的同时，不能不表现自身，不能不被评价”。