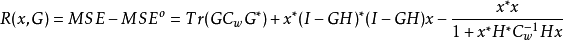在决策过程中，当某一种状态可能出现时，决策者必然要选择心中想要的方案。但如果决策者由于决策失误而没有选择心中想要的方案，则会感到遗憾和后悔。遗憾準则的基本思想就是在于儘量避免决策者的遗憾，使决策者绝不后悔。

对不确定性的理论模型选择感到遗憾，考虑到预期后果的影响。 它最初由Graham Loomes和Robert Sugden David E. Bell和Peter C. Fishburn同时开发，随后又被其他几位作者改进。

一般来说，这些模型将效用函式的遗憾术语纳入到不确定性解决方案中，对效用函式产生负面影响，并对最佳替代结果产生积极影响。 这个遗憾术语通常是减去传统效用指数的增加，连续和非负的函式。 这些类型的偏好总是违反传统意义上的传统，儘管大部分都是较弱的版本。

对激励和假设选择的若干实验证明了这种效应的大小。

第一次价格拍卖的实验表明，通过操纵参与者期望获得的反馈，观察到平均出价的显着差异。特别是，“失败者的后悔”可以通过向拍卖所有参与者揭示中标，从而向失败者揭示他们是否能够获得利润，并且可以获得多少（一个参与者有估价为50美元，出价30美元，发现中标价格为35美元，也将了解到，通过投标超过35美元，她可以赚取高达15美元）。这反过来又允许遗憾的可能性，如果投标人正确预测，如果没有提供有关中标的反馈来降低遗憾的可能性，那幺他们往往会提高出价。

在彩票决策中，实验也提供了预期遗憾的证据。如在第一次价格拍卖的情况下，对解决不确定性的反馈差异可能导致遗憾的可能性，如果这是预期的话，它可能会引起不同的偏好。例如，当面对40美元的确定性和硬币抛掷之间的选择，如果结果被正确猜测并且$ 0否则支付100美元，那幺特定的支付方式不仅可以最大限度地降低风险，而且可以遗憾，因为通常是硬币不会被抛弃（因此不确定性不能解决），而如果选择了硬币投掷，则支付0美元的结果将会引起遗憾。如果硬币被抛弃而不考虑所选择的替代方案，那幺替代收益将永远是已知的，那幺没有选择会消除遗憾的可能性。

对于人们认为自己负责的选择和行动，预期的遗憾往往被高估了。人们特别有可能高估他们在缺少期望结果的时候会感到遗憾。在一项研究中，通勤人员预测，如果他们错过了1分钟以上的火车1分钟以上的距离，而不是5分钟左右的火车，那幺他们会感到更遗憾，但实际上错过了1或5分钟火车的乘客经历了（等于）遗憾通勤员似乎高估了他们在缺少火车的时候会觉得很遗憾，因为他们倾向于低估他们将火车列入外部原因的程度（例如，丢失钱包或花更少的时间在淋浴中） 。

以下是对遗传概念如何用于设计线性估计器的说明。在这个例子中，问题是从已知噪声协方差结构的噪声线性测量中构造有限维参数向量x的线性估计器。使用均方误差（MSE）测量x的重建损失。已知未知参数矢量位于以零为中心的椭圆E中。遗憾被定义为不知道参数x的线性估计器的MSE与知道x的线性估计器的MSE之间的差异。此外，由于估计器被限制为线性，所以在后一种情况下不能实现零MSE。在这种情况下，凸最佳化问题的解决方案给出了最优的最小值遗憾线性估计器，可以通过以下参数来看待。

根据假设，观察到的矢量y和未知的确定性参数矢量x的线性模型为：

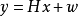
其中H是具有全列秩m的已知m×n矩阵，并且w是具有已知的零均值随机向量协方差矩阵。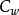

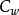
让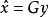：是y关于x的线性估计，其中G是某些m×n矩阵。该估计器的MSE由下式给出：

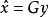
由于MSE明确地依赖于 x，因此不能直接将其最小化。相反，可以使用遗憾的概念来定义具有良好MSE性能的线性估计器。为了在这里定义遗憾，考虑知道参数x的值的线性估计器，即矩阵 G可以明确依赖于x：

的MSE是：

为了找到最佳的G（x），MSE ^ {o}相对于G是有区别的，并且使导数等于0得到：

然后，使用矩阵反转引理：

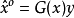
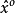
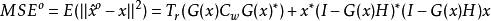
将这个G（x）替换成MSE ^ {o}，得到：

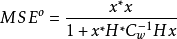
这是可以通过线性估计知道x的最小MSE。在实践中，这个MSE是无法实现的，但它作为最优MSE的约束。使用G指定的线性估计值的遗憾等于：

这里的最小值遗憾方法是最小化最坏情况的遗憾，即sup _ {x \ in E} R（x，G）。这将使参数x的最坏情况下的性能儘可能接近最佳可实现的性能。 虽然这个问题看起来很困难，但它是凸最佳化的一个例子，特别是可以有效地计算数值解。