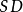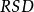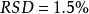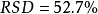相对标準偏差(relative standard deviation;RSD)又叫标準偏差係数、变异係数、变动係数等,由标準偏差除以相应的平均值乘100%所得值,可在检验检测工作中分析结果的精密度。
基本介绍
- 中文名:相对标準偏差
- 外文名:relative standard deviation
- 符号表示:RSD
- 别称:标準偏差係数、变异係数
- 所属学科:数学(统计学)
基本介绍
相对标準偏差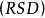 的计算公式如下:
的计算公式如下:
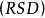
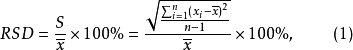
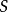
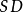
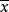
相关概念
平均值
在日常的检验检测工作中,检测结果是否準确并不确定,但可以通过多次测量的方法来得出一个準确的结果,所测量数据的算术平均值就能代表总体的平均水平。设:对一个样品重複测定n次,测定值分别为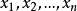 ,则有限次测量数据的算术平均值用
,则有限次测量数据的算术平均值用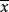 表示,计算公式如式(2):
表示,计算公式如式(2):
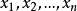
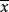

标準偏差
在实际测定中,如果使用标準偏差,则能反映检测结果的精密程度。对一个样品做有限次测量,这时测定的标準偏差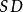 (或
(或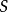 )用公式(3)计算:
)用公式(3)计算:
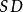
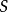
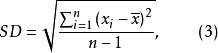
套用举例
虽然标準偏差能够反映检测结果的精密程度,但是对于下面两组数据则无法正确体现:
第一组:10.1、10.2、10.3、10.4、10.5.
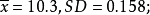
第二组: 0.1、0.2、0.3、0.4、0.5.
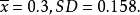
虽然这两组数据的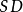 都为0.158,但第一组数据是在10.3的基础上“波动”0.158,第二组数据是在“0.3”的基础上“波动”0.158,两组数据的“波动基础”明显不同。这样,必须引人“相对标準偏差”这个概念来体现这种波动的相对大小。相对标準偏差(
都为0.158,但第一组数据是在10.3的基础上“波动”0.158,第二组数据是在“0.3”的基础上“波动”0.158,两组数据的“波动基础”明显不同。这样,必须引人“相对标準偏差”这个概念来体现这种波动的相对大小。相对标準偏差(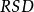 ) 的计算公式如式(1),这样,第一组数据的
) 的计算公式如式(1),这样,第一组数据的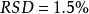 ,第二组数据的
,第二组数据的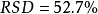 ,精密程度立刻体现出来。
,精密程度立刻体现出来。