数学中，体积形式提供了函式在不同坐标系（比如球坐标和圆柱坐标）下对体积积分的一种工具。更一般地，一个体积元是流形上一个测度。
在一个定向n-维流形上，体积元典型地由体积形式生成，所谓体积元是一个处处非零的n-阶微分形式。一个流形具有体积形式若且唯若它是可定向的，而可定向流形有无穷多个体积形式（细节见下）。
有一个推广的伪体积形式概念，对无论可否定向的流形都存在。
许多类型的流形有典範的（伪）体积形式，因为它们有额外的结构保证可选取一个更好的体积形式。在复情形，一个带有全纯体积形式的凯勒流形是卡拉比-丘流形。
基本介绍
- 中文名：体积形式
- 分类：数理科学
定义
流形M上一个体积形式是处处非0的最高阶（n-维流形上的n-形式）微分形式。
用线丛的语言来说，称最高阶外积
为行列式线丛，n-形式是它的截面。
对不可定向流形，一个体积“伪”形式，也称为“奇”或“扭曲”的体积形式，可以定义为定向丛的一个处处非0截面；这个定义同样适用于定向流形。在这种看法下，（非扭曲的）微分形式就是“偶”n-形式。除非特别地讨论扭曲形式时，我们总是略去形容词“偶”。
第一次明确地引入扭曲微分形式是德拉姆。
定向
一个流形具有体积形式若且唯若它可定向，这也可以作为可定向的一个定义。
在G-结构的语言中，一个体积形式是一个SL-结构。因为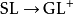
是形变收缩（因为
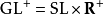，这里正实数视为纯量矩阵），一个流形具有一个SL-结构若且唯若具有一个
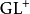-结构，即是一个定向。
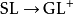
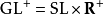
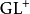
线上丛的语言中，行列式丛
的平凡性等价于可定向性，而一个线丛是平凡的若且唯若它有一个处处非0的截面，这样又得到，体积形式的存在性等价于可定向性。
对于伪体积形式，一个伪体积形式是一个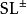
-结构，因为
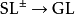同伦等价（事实上是形变收缩），任何流形都有伪体积形式。类似地，定向丛总是平凡的，所以任何流形都有一个伪体积形式。
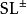
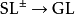
和测度的关係
任何流形有一个伪体积形式，因为定向丛（作为线丛）是平凡的。给定一个定向流形上的体积形式ω，密度 |ω| 是忘掉定向结构的非定向流形的一个伪体积形式。
任何伪体积形式ω（从而任何体积形式亦然）定义了一个波莱尔集合上一个测度：
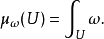
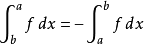
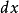
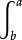
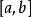
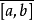
进一步，一般的测度不必连续或光滑，他们不必由体积形式定义；或更形式地说，关于一个体积形式的Radon-Nikodym导数不必绝对连续。
例子
李群
任何李群，可以由平移定义一个自然的体积形式。这就是说，如果ωe是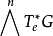
中一个元素，那幺一个左不变形式可以定义为
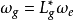，这里Lg为左平移。作为一个推论，任何李群都是可定向的。这个体积形式在相差一个常数的意义下是惟一的，相应的测度称为哈尔测度。
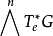
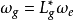
辛流形
任何辛流形（或更确切地为殆辛流形）有一个自然的体积形式。如果M是一个带有辛形式ω的2n-维流形，那幺由辛形式非退化可知ω处处非零。作为一个推论，任何辛流形是可定向的（事实上，已经定向）。
黎曼体积形式
任何黎曼流形（或伪黎曼流形）有一个自然的体积（或伪体积）形式。在局部坐标系下，能写成表达式：
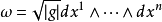
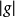
这个体积形式有许多不同的记号，包括：
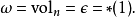
儘管希腊字母ω经常用于表示体积形式，但是这个记法很难通用，符号ω在微分几何中经常有其它意思（比如辛形式），所以一个公式中的ω不一定就表示体积形式。
一个流形如果既是辛的又是黎曼的，如果流形是凯勒的那种方式定义的体积形式相等。