传说在阿基米德晚年,在叙拉古与它的盟国罗马共和国分裂后,罗马派了一支舰队来围城。
基本介绍
- 中文名:圆柱容球
- 属性:几何图形
- 地点:阿基米德的墓碑
- 时间:公元前212年
背景
当时阿基米德负责城防工作,他设计製造了一些灵巧的机械来摧毁敌人的舰队。他用投火器将燃烧的东西弹出去烧敌人的船舰,用一些起重机械把敌人的船只吊起掀翻,以至后来罗马人甚至不敢过分靠近城墙,只要看见城墙出现象绳子之类的玩意儿,就吓得赶快逃跑。 然而三年以后,即在公元前212年,该城还是被攻陷了。 据说罗马兵入城时,统帅马塞拉斯出于敬佩阿基米德的才能,曾下令不準伤害这位贤能。而阿基米德似乎并不知道城池已破,又重新沉迷于数学的深思之中。 一个罗马士兵突然出现在他面前,命令他到马塞拉斯那里去,遭到阿基米德的严词拒绝,于是阿基米德不幸死在了这个士兵的刀剑之下。 另一种说法是:罗马士兵闯入阿基米德的住宅,看见一位老人在地上埋头作几何图形(还有一种说法他在沙滩上画图),士兵将图踩坏,阿基米德怒斥士兵:"不要弄坏我的圆!"士兵拔出短剑,这位旷世绝伦的大科学家,竟如此地在愚昧无知的罗马士兵手下丧生了。 马塞拉斯对于阿基米德的死深感悲痛。他将杀死阿基米德的士兵当作杀人犯予以处决,并为阿基米德修了一座陵墓,在墓碑上根据阿基米德生前的遗愿,刻上了"圆柱容球"这一几何图形。 随着时间的流逝,阿基米德的陵墓被荒草湮没了。后来,西西里岛的会计官、政治家、哲学家西塞罗(公元前106~前43年)游历叙拉古时,在荒草发现了一块刻有圆柱容球图形的墓碑,依此辩认出这就是阿基米德的坟墓,并将它重新修复了。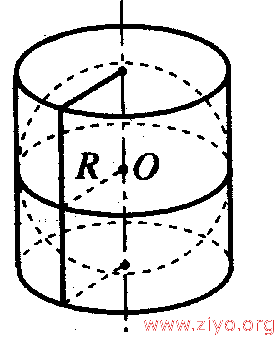

证明公式
球的表面积及体积计算公式: V球=4/3πr^3;S球=4πr^2。(r为球的半径)
讨论:公式的特点;球面是否可展开为一个平面图形? (证明的基本思想是:“分割→求体积和→求极限→求得结果”,以后的学习中再证明球的公式)
练习:一个气球的体积扩大2倍,那幺它的表面积、体积分别扩大多少倍? 2. 体积公式的实际套用:
示例:一种空心钢球的质量是142g,外径是5.0cm,求它的内径. (钢密度7.9kg/cm3)
讨论:如何求空心钢球的体积?
讨论:公式的特点;球面是否可展开为一个平面图形? (证明的基本思想是:“分割→求体积和→求极限→求得结果”,以后的学习中再证明球的公式)
练习:一个气球的体积扩大2倍,那幺它的表面积、体积分别扩大多少倍? 2. 体积公式的实际套用:
示例:一种空心钢球的质量是142g,外径是5.0cm,求它的内径. (钢密度7.9kg/cm3)
讨论:如何求空心钢球的体积?
列式计算 → 小结:体积套用问题.
示例:有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放入一个半径为R的球,并注入水,使水面与球正好相切,然后将球取出,求此时容器中水的深度.
圆柱容球定理是这样的:
圆及其外切正方形绕图中由虚线表示的对称轴旋转一周生成的几何体称为圆柱容球。在圆柱容球中,球的体积是圆柱体积的三分之二,球的表面积也是圆柱全面积的三分之二。
在今天看来这个定理不难证明,事实上:
设圆的半径为R,球的体积与圆柱的体积分别为V球及V柱,球的表面积与圆柱的全面积分别为S球及S柱,则有:
V柱=底面积×高=πr^2×2r=2πr^3
示例:有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放入一个半径为R的球,并注入水,使水面与球正好相切,然后将球取出,求此时容器中水的深度.
圆柱容球定理是这样的:
圆及其外切正方形绕图中由虚线表示的对称轴旋转一周生成的几何体称为圆柱容球。在圆柱容球中,球的体积是圆柱体积的三分之二,球的表面积也是圆柱全面积的三分之二。
在今天看来这个定理不难证明,事实上:
设圆的半径为R,球的体积与圆柱的体积分别为V球及V柱,球的表面积与圆柱的全面积分别为S球及S柱,则有:
V柱=底面积×高=πr^2×2r=2πr^3
V球=4/3πr^2
V球=2/3V柱
S柱=侧面积+上下底面积=2πr×2r+2πr^2=6πr^2
S柱=侧面积+上下底面积=2πr×2r+2πr^2=6πr^2
S球=4πr^2
S球=2/3S柱
证明方法
在当时并不知道球的面积和体积公式,阿基米德用穷竭法来解决面积问题,用槓桿法来解决体积问题
设一圆柱竖直放立水平平面上,底面直径等于高等于2r,中有一内切球,另有底面半径为2r的顶点在圆柱上底中心的圆锥。圆锥底面与圆柱下底共面。
用两两相距极近的一组水平平面截这三个立体任取离圆锥顶为h的一片,它厚为Δh。把球上的那片和圆锥上的那片挂在支点在中点,全长为4r的槓桿的左端上,把柱上的那片挂在支点右侧距支点h的点处。
我们可知道,当h足够小时,三者相差无几。
即
V球片≈Δh[πh﹙2r﹣h﹚]
V锥片≈Δhπh2
柱片体积为 V柱片=Δhπr2
设密度皆为1则球片与锥片形成的力矩的绝对值为
2r [πh﹙2r-h﹚+πh2Δ]Δh=4πhΔhr2
上式右端正好有柱片的 力矩的绝对值 ,4为平衡係数。
若将一切碎片都如上挂在槓桿上,则左端的总力矩绝对值为
2r[V球+V锥]
右端的总力矩的4倍为rV柱,而V柱形成的理据是质量集中在其重心,其力臂为重心到支点Oˊ的距离r。
即
2r[V球+V锥]=4rV柱 ①
又已知V锥=8r3/3,V柱=2πr3,
代入①得
V球=4πr3/3
用两两相距极近的一组水平平面截这三个立体任取离圆锥顶为h的一片,它厚为Δh。把球上的那片和圆锥上的那片挂在支点在中点,全长为4r的槓桿的左端上,把柱上的那片挂在支点右侧距支点h的点处。
我们可知道,当h足够小时,三者相差无几。
即
V球片≈Δh[πh﹙2r﹣h﹚]
V锥片≈Δhπh2
柱片体积为 V柱片=Δhπr2
设密度皆为1则球片与锥片形成的力矩的绝对值为
2r [πh﹙2r-h﹚+πh2Δ]Δh=4πhΔhr2
上式右端正好有柱片的 力矩的绝对值 ,4为平衡係数。
若将一切碎片都如上挂在槓桿上,则左端的总力矩绝对值为
2r[V球+V锥]
右端的总力矩的4倍为rV柱,而V柱形成的理据是质量集中在其重心,其力臂为重心到支点Oˊ的距离r。
即
2r[V球+V锥]=4rV柱 ①
又已知V锥=8r3/3,V柱=2πr3,
代入①得
V球=4πr3/3