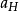右图为将太空船从低轨道（1）送往较高轨道（3）的霍曼转移轨道。太空船在原先轨道（1）上瞬间加速后，进入一个椭圆形的转移轨道（2）。太空船由此椭圆轨道的近拱点开始，抵达远拱点后再瞬间加速，进入另一个圆轨道（3），此即为目标轨道。要注意的是，三个轨道的轨道半长轴是越来越大，因此两次引擎推进皆是加速，总能量增加而进入较高（半长轴较大）的轨道。

图1.霍曼转移轨道为图中编号2的半椭圆轨道

反过来，霍曼转移轨道亦可将太空船送往较低的轨道，不过是两次减速而非加速。

霍曼转移轨道的两次加速假设是瞬间完成，但实际上加速要花时间，因此需要额外的燃料来补偿。使用高推力引擎所需额外燃料较小，低推力引擎则还要以控制推进时间、逐渐提高轨道来逼近霍曼转移轨道。因此实际上ΔV会比假设情况更大且花更多时间。

轨道上物体的总能等于动能与重力位能的和，而总能又等于重力位能（轨道半径为轨道半长轴a时的重力位能）的一半：

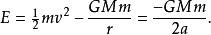
以速度为未知解方程式，得到轨道能量守衡方程式：

其中，v为物体的速度，为中央物体的标準重力参数，r为物体至中央物体中心的距离，a为物体轨道的半长轴。

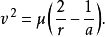
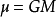
因此霍曼转移所需的两次ΔV为（假设速度改变是瞬间达成）：

分别是原本圆轨道与目标圆轨道的半径，其中大的（小的）对应到霍曼转移轨道的远拱点（近拱点）距离。

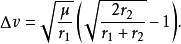
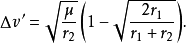
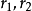
无论前往较高或较低轨道，根据克卜勒第三定律，霍曼转移所花的时间为：

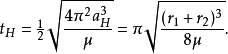
（即椭圆轨道周期的一半），其中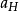是霍曼转移轨道的半长轴。