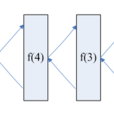
递归定理(recursion theorem)亦称不动点定理。反映部分递归函式类基本性质的重要定理。最初是由美国逻辑学家、数学家克林(Kleene, S. C.)于1938年证明的，克林所给的递归定理的原始形式特称为第二递归定理)：若\varphi为部分递归函式，则存在e使得\alpha_{e}(x)=\varphi(e,x)。
基本介绍
- 中文名：递归定理
- 外文名：recursion theorem
- 领域：数学
- 适用对象：递归函式
- 别称：不动点定理、第二递归定理
- 首次证明：美国数学家克林
递归
当事物根据其本身或其类型进行定义时，就会发生递归。 递归用于从语言学到逻辑的各种学科。 递归的最常见的套用是数学和计算机科学，其中定义的函式在其自己的定义中被套用。 虽然这显然定义了无限数量的实例（函式值），但它通常以这样的方式完成，即不会发生循环或无限链引用。
定义
递归是程式在其中一个步骤涉及调用过程本身时所经历的过程。递归的过程被称为“递归过程”。
要理解递归，必须认识到一个过程和一个过程的运行之间的区别。程式是基于一组规则的一组步骤。程式的运行涉及实际遵循规则并执行步骤。类比：程式就像书面食谱;运行程式就像实际準备饭菜一样。
递归与执行某些其他过程的过程规範中的引用相关，但与之不同。例如，食谱可能指的是烹饪蔬菜，这是另一种程式，又需要加热水等等。然而，一个递归过程是（至少）其中一个步骤中的一个步骤需要一个相同过程的新实例，就像一个sourdough配方调用最后一次同一个配方所剩下的一些麵团。这当然会立即产生无限循环的可能性;如果在某些情况下跳过有问题的步骤，则可以在定义中正确使用递归，因为该过程可以完成，就像一个sourdough配方，也告诉你如何获得一些起始麵团，以防万一你从未做过。即使正确定义，递归过程对于人类来说也不容易，因为它需要区分新的与过程的（部分执行的）调用;这需要对各种同时进行的程式的实现进行一些管理。因此，递归定义在日常情况下非常罕见。一个例子可能是以下程式找到一条通过迷宫的方式。继续前进，直到到达出口或分支点（死端被认为是具有0个分支的分支点）。如果达到的点是退出，终止。否则反覆尝试每个分支，递归地使用该过程;如果每次试验都没有达到死胡同，就返回到导致这个分支点的路径并报告失败。这是否实际上定义了终止程式取决于迷宫的性质：它不能允许循环。在任何情况下，执行该过程需要仔细记录所有当前探索的分支点，并且哪些分支已经被彻底地尝试。
定理表述
递归定理的原始形式（特称为第二递归定理）为：若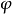
为部分递归函式，则存在e，使得
。
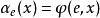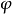
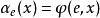
与第二递归定理等价的是下列不动点定理：对任何递归函式f，存在自然数n(称为f的不动点)，使φn=φf(n)。不动点定理有一些推广的形式：
- 带参数的递归定理。若f为n+1元递归函式，则存在一一的n元递归函式h，使
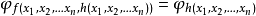
2.二重递归定理.对递归函式f，g，存在自然数a，b，使得：φa=φf(a，b)& φb=φg(a，b).
对一个递归函式f，其不动点不仅存在，而且一定有无穷多个，它们所组成的集合可能是递归集，也可能是非递归的.值得指出的是，对部分递归函式，其不动点定理与第二递归定理是等价的，但两者的证明所需要的基础并不一样.前者依赖于Sm定理和枚举定理，而后者则仅依赖于Sm定理.因此，若一个函式类具有Sm性质但不具有枚举性(如原始递归函式类)，则第二递归定理对它也成立，而不动点定理则不然.与第二递归定理相对应的是关于部分递归泛函的第一不动点定理(美国逻辑学家、数学家克林(Kleene，S.C.)，于1952年证明的)：设F(α，x)为部分递归泛函，则存在一个部分递归函式α，使得：
1.ᗄx(α(x)=F(α，x));
2.ᗄx(β(x)=F(β，x))→α⊆β;
此时α称为F的最小不动点。第一和第二不动点定理之名称纯粹是由克林的经典着作《元数学导论》中表述的先后次序而定的，别无他意。此外，在许多文献中，上述的(第二)不动点定理也称为递归定理而不加区分。