递归做为一种算法在程式设计语言中广泛套用。是指函式/过程/子程式在运行过程中直接或间接调用自身而产生的重入现象。递归是计算机科学的一个重要概念,递归的方法是程式设计中有效的方法,採用递归编写程式能使程式变得简洁和清晰。。
递归算法是把问题转化为规模缩小了的同类问题的子问题。然后递归调用函式(或过程)来表示问题的解。
基本介绍
- 中文名:递归运算法
- 外文名:Recursive Arithmetic
摘要
递归做为一种算法在程式设计语言中广泛套用。是指函式/过程/子程式在运行过程中直接或间接调用自身而产生的重入现象。递归是计算机科学的一个重要概念,递归的方法是程式设计中有效的方法,採用递归编写程式能使程式变得简洁和清晰。。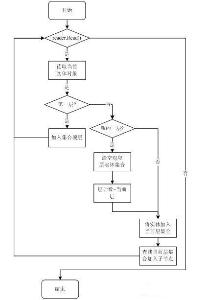 图片
图片
 图片
图片递归算法是把问题转化为规模缩小了的同类问题的子问题。然后递归调用函式(或过程)来表示问题的解。
定义
程式调用自身的编程技巧称为递归( recursion)。
一个过程或函式在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型複杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程式就可描述出解题过程所需要的多次重複计算,大大地减少了程式的代码量。
递归的能力在于用有限的语句来定义对象的无限集合。一般来说,递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时,递归前进;当边界条件满足时,递归返回。
注意:
(1) 递归就是在过程或函数里调用自身;
(2) 在使用递归策略时,必须有一个明确的递归结束条件,称为递归出口。
递归的另一种定义:
递归,就是用自己的简单情况,定义自己。
在数学和计算机科学中,递归指由一种(或多种)简单的基本情况定义的一类对象或方法,并规定其他所有情况都能被还原为其基本情况。
斐波那契数列是典型的递归案例:Fib(0) = 0 [基本情况] Fib(1) = 1 [基本情况] 对所有n > 1的整数:Fib(n) = (Fib(n-1) + Fib(n-2)) [递归定义] 儘管有许多数学函式均可以递归表示,但在实际套用中,递归定义的高开销往往会让人望而却步。
例如:阶乘(1) = 1 [基本情况] 对所有n > 1的整数:阶乘(n) = (n * 阶乘(n-1)) [递归定义] 一种便于理解的心理模型,是认为递归定义对对象的定义是按照“先前定义的”同类对象来定义的。
例如:你怎样才能移动100个箱子?答案:你首先移动一个箱子,并记下它移动到的位置,然后再去解决较小的问题:你怎样才能移动99个箱子?最终,你的问题将变为怎样移动一个箱子,而这是你已经知道该怎幺做的。
如此的定义在数学中十分常见。例如,集合论对自然数的正式定义是:1是一个自然数,每个自然数都有一个后继,这一个后继也是自然数。
算法
递归过程一般通过函式或子过程来实现。递归算法:在函式或子过程的内部,直接或者间接地调用自己的算法。
递归算法的特点
递归算法是一种直接或者间接地调用自身的算法。在计算机编写程式中,递归算法对解决一大类问题是十分有效的,它往往使算法的描述简洁而且易于理解。
递归算法是一种直接或者间接地调用自身的算法。在计算机编写程式中,递归算法对解决一大类问题是十分有效的,它往往使算法的描述简洁而且易于理解。
递归算法解决问题的特点:
(1) 递归就是在过程或函数里调用自身。
(2) 在使用递归策略时,必须有一个明确的递归结束条件,称为递归出口。
(3) 递归算法解题通常显得很简洁,但递归算法解题的运行效率较低。所以一般不提倡用递归算法设计程式。
(4) 在递归调用的过程当中系统为每一层的返回点、局部量等开闢了栈来存储。递归次数过多容易造成栈溢出等。所以一般不提倡用递归算法设计程式。
递归算法要求
递归算法所体现的“重複”一般有三个要求:
递归算法要求
递归算法所体现的“重複”一般有三个要求:
一是每次调用在规模上都有所缩小(通常是减半);
二是相邻两次重複之间有紧密的联繫,前一次要为后一次做準备(通常前一次的输出就作为后一次的输入);
三是在问题的规模极小时必须用直接给出解答而不再进行递归调用,因而每次递归调用都是有条件的(以规模未达到直接解答的大小为条件),无条件递归调用将会成为死循环而不能正常结束。
套用
递归算法一般用于解决三类问题:
(1)数据的定义是按递归定义的。(Fibonacci函式)
(2)问题解法按递归算法实现。(回溯)
(3)数据的结构形式是按递归定义的。(树的遍历,图的搜寻)
递归的缺点: 递归算法解题相对常用的算法如普通循环等,运行效率较低。因此,应该儘量避免使用递归,除非没有更好的算法或者某种特定情况,递归更为适合的时候。在递归调用的过程当中系统为每一层的返回点、局部量等开闢了栈来存储。递归次数过多容易造成栈溢出等。
实例
比如:运用递归算法查询多个上下级关係树的数据结构中的数据(C# 语法)
 图片
图片privateviod GET()
{
int Count= 0;
Count = GetCount(1,ProductCount);
}
private int GetCount(int ParentID, int ProductCount)
{
string sqlString = "SELECT* FROM表 WHERE ID=" + ParentID;
Model model = BLL.GetModel(sqlString); //BLL.GetModel()是自定义方法
if(model != null) //条件
{
Count += model.Count;
GetCount(model.ID,Count); //递归
}
else
{
return Count;
}
//备注:当递归查询完所有的上下级关係树,该递归才会结束,才会返回Count
}
网页中的套用
在网站开发中,递归算法大量套用于无限级分类
