递归调用是一种特殊的嵌套调用,是某个函式调用自己或者是调用其他函式后再次调用自己的,只要函式之间互相调用能产生循环的则一定是递归调用,递归调用一种解决方案,一种是逻辑思想,将一个大工作分为逐渐减小的小工作,比如说一个和尚要搬50块石头,他想,只要先搬走49块,那剩下的一块就能搬完了,然后考虑那49块,只要先搬走48块,那剩下的一块就能搬完了,递归是一种思想,只不过在程式中,就是依靠函式嵌套这个特性来实现了。
基本介绍
- 中文名:递归调用
- 外文名:recursive invocation
- 函式模型:fun(形参)
- 递归举例:计算阶乘的代码
基本信息
定义
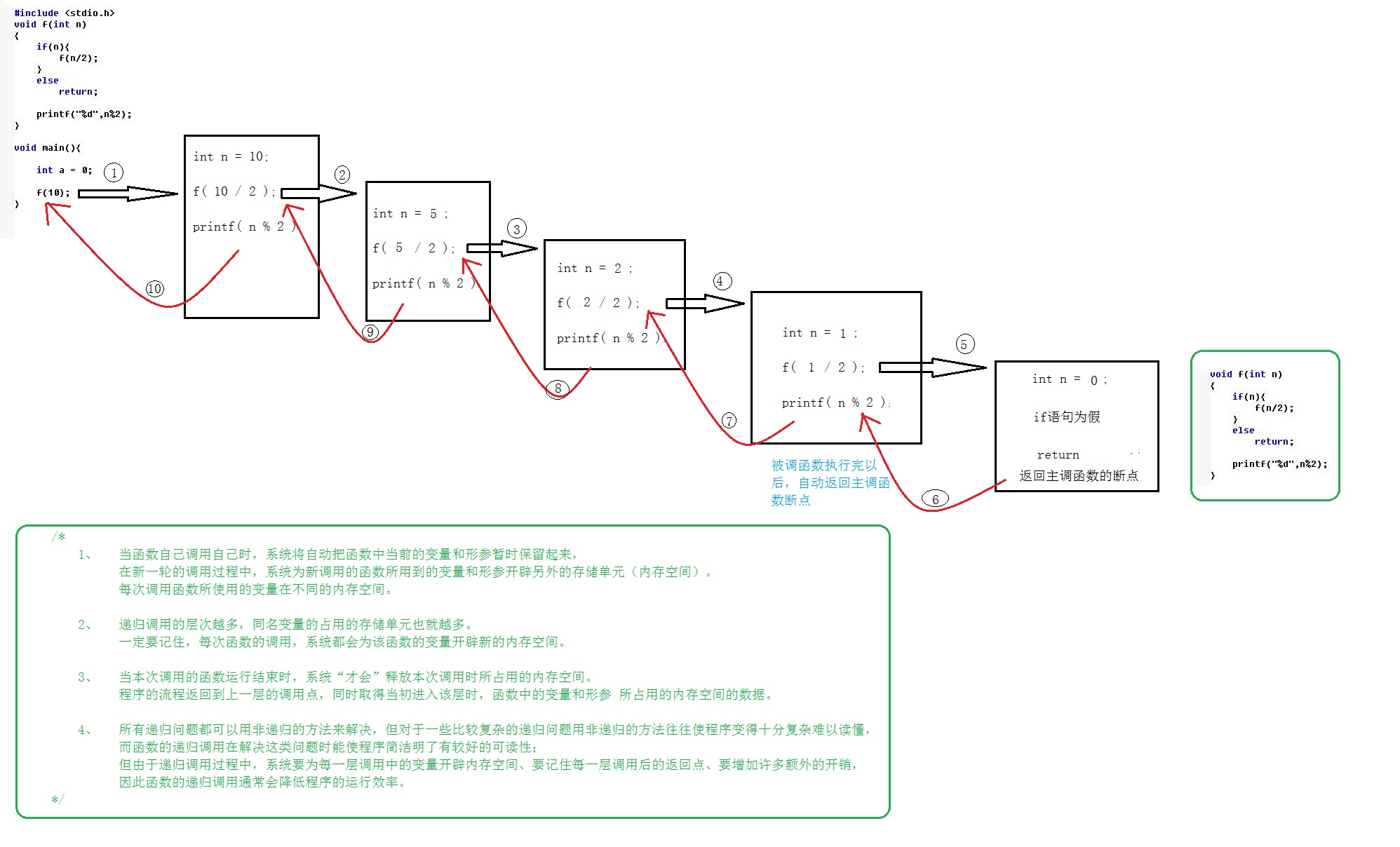
递归调用就是在当前的函式中调用当前的函式并传给相应的参数,这是一个动作,这一动作是层层进行的,直到满足一般情况的的时候,才停止递归调用,开始从最后一个递归调用返回。

英文
recursive invocation
函式模型
fun(形参){
fun(参数值1) //第一次递归调用
fun(参数值2) //第二次递归调用
递归举例
C语言中的递归
计算阶乘的代码
long fact(long n)
{
if(n==0||n==1) return 1L;
else return n*fact(n-1);
}
这个函式叫做fact,它自己调用自己,这个就是一个典型的递归调用,调用过程类似一个栈。
注: 主调函式又是被调函式。执行递归函式将反覆调用其自身。 每调用一次就进入新的一层。
int f (int x)
{
int y;
z=f(y);
return z;
} 这个函式是一个递归函式。 但是运行该函式将无休止地调用其自身,这当然是不正确的。为了防止递归调用无终止地进行, 必须在函式内有终止递归调用的手段。常用的办法是加条件判断, 满足某种条件后就不再作递归调用,然后逐层返回。 下面举例说明递归调用的执行过程。
注:鍊表在某种程度上就是递归的调用.
Pascal中的递归
const
z=10000;
var
a:array[0..z+1]of integer;
n,j,i,k:longint;
begin
readln(n);write(n,'!=');
begin
a[1]:=1;
for i:=1 to n do
begin
for j:=1 to z do
a[j]:=a[j]*i;
for k:=1 to z do
begin
a[k+1]:=a[k+1]+a[k]div 10;
a[k]:=a[k]mod 10;
end;
end;
i:=z;k:=0;
repeat
if a[i]<>0 then k:=1;
i:=i-1;
until k=1;
k:=0;
for j:=i+1 downto 1 do
write(a[j]);
end;
writeln;
end.
c++语言中的递归
#include<iostream>
using namespace std;
int fac(int n)
{
int s=1;
for (int i=n;i>0;i--)
{
if (s<=s*i) s=s*i;
else
{
cout<<"over int area"<<endl;
return 0;
};
}
return s;
}
void main()
JAVA写的递归调用
public class TestDg {
public static void main(String[] args) {
System.out.println(method(5));
}
public static int method(int n) {
if (n == 1)
return 1;
else
return n * method(n - 1);
}
}
汉诺塔------软体递归调用里面最经典的一个案例
#include<stdio.h>
int c=0; /* 全局变数,搬动次数 */
void move(char x,int n,char z)
{ /* 第n个圆盘从塔座x搬到塔座z */
printf("第%i步: 将%i号盘从%c移到%c\n",++c,n,x,z);
}
void hanoi(int n,char x,char y,char z)
{ /* 将塔座x上按直径由小到大且自上而下编号为1至n的n个圆盘 */
/* 按规则搬到塔座z上。y可用作辅助塔座 */
if(n==1)
move(x,1,z); /* 将编号为1的圆盘从x移到z */
else
{
hanoi(n-1,x,z,y); /* 将x上编号为1至n-1的圆盘移到y,z作辅助塔 */
move(x,n,z); /* 将编号为n的圆盘从x移到z */
hanoi(n-1,y,x,z); /* 将y上编号为1至n-1的圆盘移到z,x作辅助塔 */
}
}
void main()
{
int n;
printf("3个塔座为a、b、c,圆盘最初在a座,藉助b座移到c座。请输入圆盘数:");
scanf("%d",&n);
hanoi(n,'a','b','c');
}
递归详解
调用前
一个函式的运行期间调用另一个函式时,在运行被调用函式之前,系统需要完成3件事情:
(1)将所有的实参、返回地址等信息传递给被调用函式保存;
(2)为被调用函式的局部变数分配存储区;
(3)将控制转移到被调函式的入口。
调用中
而从被调用函式返回调用函式之前,系统也应完成3件工作:
(1)保存被调函式的计算结果;
(2)释放被调函式的数据区;
(3)依照被调函式保存的返回地址将控制转移到调用函式。当有多个函式构成嵌套调用时,按照后调用先返回的原则。
递归函式特点
所有递归函式的结构都是类似的。
(1)函式要直接或间接调用自身。
(2)要有递归终止条件检查,即递归终止的条件被满足后,则不再调用自身函式。
(3)如果不满足递归终止的条件,则调用涉及递归调用的表达式。在调用函式自身时,有关终止条件的参数要发生变化,而且需向递归终止的方向变化。
总结
函式的调用原则和数据结构栈的实现是相一致。也说明函式调用是通过栈实现的。