程式语言中,函式Func(Type a,……)直接或间接调用函式本身,则该函式称为递归函式。递归函式不能定义为内联函式。
在数学上,关于递归函式的定义如下:对于某一函式f(x),其定义域是集合A,那幺若对于A集合中的某一个值X0,其函式值f(x0)由f(f(x0))决定,那幺就称f(x)为递归函式。
基本介绍
- 中文名:递归函式
- 外文名:recursive function
- 类别:从自然数到自然数的函式
- 定义:直接或间接调用函式本身
定义
一种计算过程,如果其中每一步都要用到前一步或前几步的结果,称为递归的。用递归过程定义的函式,称为递归函式,例如连加、连乘及阶乘等。凡是递归的函式,都是可计算的,即能行的。
古典递归函式,是一种定义在自然数集合上的函式,它的未知值往往要通过有限次运算回归到已知值来求出,故称为“递归”。它是古典递归函式论的研究对象。
介绍
在数理逻辑和计算机科学中,递归函式或μ-递归函式是一类从自然数到自然数的函式,它是在某种直觉意义上是"可计算的" 。事实上,在可计算性理论中证明了递归函式精确的是图灵机的可计算函式。递归函式有关于原始递归函式,并且它们的归纳定义(见下)建造在原始递归函式之上。但是,不是所有递归函式都是原始递归函式 — 最着名的这种函式是阿克曼函式。
其他等价的函式类是λ-递归函式和马尔可夫算法可计算的函式。
一个直接的例子
//代码1void func(){//...if(...)func();lse//...}条件
一个含直接或间接调用本函式语句的函式被称之为递归函式,在上面的例子中能够看出,它必须满足以下两个条件:
1) 在每一次调用自己时,必须是(在某种意义上)更接近于解;
2) 必须有一个终止处理或计算的準则。
例如:
梵塔的递归函式
//Cvoid hanoi(int n,char x,char y,char z){if(n==1)move(x,1,z);else{hanoi(n-1,x,z,y);move(x,n,z);hanoi(n-1,y,x,z);}}阶乘的递归函式,公式如下: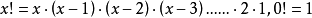
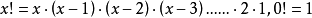
//C++int Factorial(int n){if(n==0||n==1)return 1;elsereturn n * Factorial(n-1)}计算
函式的概念是一个很一般的概念。在定义函式时,不一定要具体给出通过自变数求函式值的方法。因此,可将函式分成两类,一类是所谓能行可计算函式,另一类是非能行可计算的函式。这前一种函式无论在理论上或在实际上都是非常重要的,因此人们便试图给它们以精确的数学刻画。递归函式便是许多这种刻画中的一种。
我们以下考虑的函式都是从自然数到自然数的函式。
我们先定义几个初等函式
(1)零函式 Z(x)=0;
(2)后继函式 S(x)=x+1;
(3)广义幺函式 U1n(x1,…xn)=xi;
显然,上面这些函式都是能行可计算的。
再介绍几个将函式变换为函式的运算元。
(1)複合运算元 设f是n元函式,g1…gn是m元函式,複合运算元将f,g1…gn变换成为如下的m元函式h:
h(x1…xm)=f1g1(x1,…xm),…gn(x1,…xm))
(2)递归运算元 设f是n元函式 (≥0),g是n+2元函式,递归运算元将f,g变换成满足下列条件的h+1元函式h:
h(x1,…,xn,0)=f(x1,…xn)
h(x1,…xn,y+1)=g(x1,…xn,y,h(x1,…xn))
(3)μ一运算元,设f是n+1元函式,如果存在y,使f(x1,…xn,y)=0,我们以μyf(x1…xny)表示这样的y中的最小者,如果使f(x1…xny)=0的y不存在,我们说μyf(x1,…xny)无定义。μ-运算元将n+1元函式f变换成下面的几元函式h
h(x1,…xn)=μyf(x1…xny)
注意,μ运算元可以将一个全函式变换成一个部分函式(即在自然数的某个子集上有定义的函式)。
可以看出,上述所有运算元都是将能行可计算函式变换为能行可计算函式。
所谓递归函式类便是包含零函式、广义幺函式,并在複合运算元、递归运算元,μ-运算元下封闲的最小函式类。
容易相信,任何递归函式都是能行可计算的。反过来,是否存在直观上能行可计算的,但不是递归的函式呢?人们直到现在还没有发现这样的函式。相反,人们证明了,现已遇到的直观上能行可计算的函式都是递归函式。进一步,人们还证明了,递归函式类与其他的一些刻画能行可计算函式的方法产生的函式类是完全一致的,这些事实促使车尔赤(Church)提出了他的着名的论点:
递归函式类与直观能行可计算函式类是重合的。
这个论点已被大多数递归论学者所接受。
例子
【pascal语言】
//使用VB代码格式,实际为Pascalfunctiondo(x:integer);beginifx<=1thenexit(0)elseifx>1thenexit(do(x-1)+10)end;

