递归算法(英语:recursion algorithm)在计算机科学中是指一种通过重複将问题分解为同类的子问题而解决问题的方法。递归式方法可以被用于解决很多的计算机科学问题,因此它是计算机科学中十分重要的一个概念。绝大多数程式语言支持函式的自调用,在这些语言中函式可以通过调用自身来进行递归。计算理论可以证明递归的作用可以完全取代循环,因此在很多函式程式语言(如Scheme)中习惯用递归来实现循环。
基本介绍
- 中文名:递归算法
- 外文名:recursive algorithm
- 属性:计算机算法
- 实现过程:一般通过函式或子过程来实现
- 特点:递归就是在过程或函数里调用自身
递归程式
在支持自调用的程式语言中,递归可以通过简单的函式调用来完成,如计算阶乘的程式在数学上可以定义为:
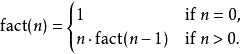
(define (factorial n) (if (= n 0) 1 (* n (factorial (- n 1)))))
不动点组合子
即使一个程式语言不支持自调用,如果在这语言中函式是第一类对象(即可以在运行期创建并作为变数处理),递归可以通过不动点组合子(英语:Fixed-point combinator)来产生。以下Scheme程式没有用到自调用,但是利用了一个叫做Z 运算元(英语:Z combinator)的不动点组合子,因此同样能达到递归的目的。
(define Z (lambda (f) ((lambda (recur) (f (lambda arg (apply (recur recur) arg)))) (lambda (recur) (f (lambda arg (apply (recur recur) arg)))))))(define fact (Z (lambda (f) (lambda (n) (if (<= n 0) 1 (* n (f (- n 1))))))))
这一程式思路是,既然在这里函式不能调用其自身,我们可以用 Z 组合子套用(application)这个函式后得到的函式再套用需计算的参数。
尾部递归
尾部递归是指递归函式在调用自身后直接传回其值,而不对其再加运算。尾部递归与循环是等价的,而且在一些语言(如Scheme中)可以被最佳化为循环指令。 因此,在这些语言中尾部递归不会占用调用堆叠空间。以下Scheme程式同样计算一个数字的阶乘,但是使用尾部递归:
(define (factorial n) (define (iter product counter) (if (> counter n) product (iter (* counter product) (+ counter 1)))) (iter 1 1))
能够解决的问题
- 数据的定义是按递归定义的。如Fibonacci函式。
- 问题解法按递归算法实现。如Hanoi问题。
- 数据的结构形式是按递归定义的。如二叉树、广义表等。
递归数据
数据类型可以通过递归来进行定义,比如一个简单的递归定义为自然数的定义:“一个自然数或等于0,或等于另一个自然数加上1”。Haskell中可以定义鍊表为:
data ListOfStrings = EmptyList | Cons String ListOfStrings
这一定义相当于宣告“一个鍊表或是空串列,或是一个鍊表之前加上一个字元串”。可以看出所有鍊表都可以通过这一递归定义来达到。
