连续型随机变数是指如果随机变数X的所有可能取值不可以逐个列举出来，而是取数轴上某一区间内的任一点的随机变数。例如，一批电子元件的寿命、实际中常遇到的测量误差等都是连续型随机变数。
基本介绍
- 中文名：连续型随机变数
- 外文名：Continuous random variable
- 领域：数学
- 类别：数学概念
数学定义
对于随机变数X，若存在一个非负的可积函式f(x)，使得对任意实数x，有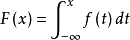
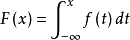
则称X为连续性随机变数。其中f(x)为X的机率分布密度函式，简称机率密度记为X～f(x)。
相关性质
由定义可知，
- 若f（x）在点x连续，则有F’（x）=f（x）
- f（x）是可积，则它的原函式F（x）连续；
3.对于任意两个实数x1，x2（假设x1<x2），都有：
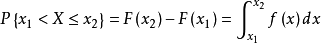
X取任一指定实数值a的机率，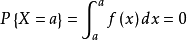
,这样在计算连续性随机变数落在某一区间的机率时，可以不必区分该区间是开区间还是闭区间。
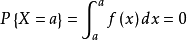
有
儘管P{X=a}=0，但{X=a}并不是不可能事件。同样，一个事件的机率为1，并不意味这个事件一定是必然事件。
当提到一个随机变数X的机率分布，指的是它的分布函式，当X是连续型时指的是它的机率密度，当X是离散型时指的是它的分布律。
概念辨析
能按一定次序一一列出，其值域为一个或若干个有限或无限区间，这样的随机变数称为离散型随机变数。离散型随机变数与连续型随机变数也是由随机变数取值範围（或说成取值的形式）确定，变数取值只能取离散型的自然数，就是离散型随机变数。
实例
比如，一次掷20个硬币，k个硬币正面朝上，
k是随机变数，
k的取值只能是自然数0，1，2，…，20，而不能取小数3.5、无理数√20……
因而k是离散型随机变数。
再比如，掷一个骰子，令X为掷出的结果，则只会有1,2,3,4,5,6这六种结果，而掷出3.3333是不可能的。
因而X也是离散型随机变数。
如果变数可以在某个区间内取任一实数，即变数的取值可以是连续的，这随机变数就称为连续型随机变数。
比如，公共汽车每15分钟一班，某人在站台等车时间x是个随机变数，
x的取值範围是[0,15)，它是一个区间，从理论上说在这个区间内可取任一实数3分钟、5分钟7毫秒、7√2分钟，在这十五分钟的时间轴上任取一点，都可能是等车的时间，因而称这随机变数是连续型随机变数。