递归定义是数理逻辑和计算机科学用到的一种定义方式，使用被定义对象的自身来为其下定义（简单说就是自我複製的定义）。递归定义与归纳定义类似，但也有不同之处。递归定义中使用被定义对象自身来定义，而归纳定义是使用被定义对象的已经定义的部分来定义尚未定义的部分。不过，使用递归定义的函式或集合，它们的性质可以用数学归纳法，通过递归定义的内容来证明。

大部分的递归定义都由三个部分构成：基本情况的定义，递归法则和递归结束的情况。如果定义的对象是无限的，那幺可以省略第三个部分（递归结束的情况）。比如说，可以用递归定义的方式来定义如下的一个自然数集上的函式f：

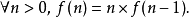
这个定义在逻辑上是成立的，因为它首先定义了f在最小的自然数0上的取值，接下来对每个大于零的自然数n，只要重複有限多次定义的过程，最终就会回到对0的定义上。这样定义出的函式f就是阶乘函式。

递归定义和循环定义的不同之处在于，后者不包括对基本情况的定义。比如定义建立在整数集上的函式g：

则我们永远无法确定g的取值，这便是循环定义。

它由两个部分组成：

1.初始条件：列出哪些个体属于一个给定的集合，

2.归纳条件：当在条件中列出的个体属于给定集合时，则另一些个体也属于该集合。

例如，在命题逻辑中，合式公式定义为：

合式公式是按以下规则构成的有穷长符号串：

1.每个原子公式是合式公式，

2.若A是合式公式，则是合式公式，

3.若A,B是合式公式，则是合式公式，

4.若A是合式公式，x是变元，则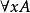是合式公式。