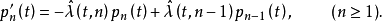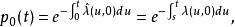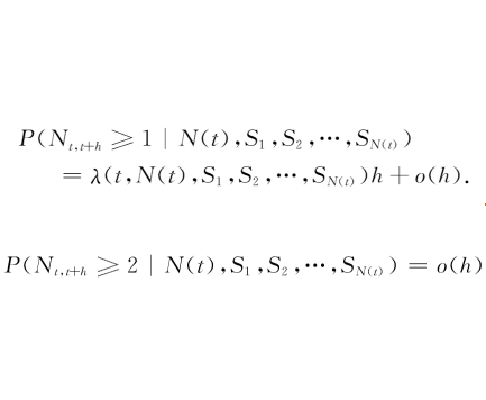自激点过程(self-exciting point process)是一类强度可以依赖于过程自身历史的点过程.齐次泊松过程的强度是一常数,如果允许强度随时间t改变就得到带时倚强度的泊松过程。如果再允许强度在任一时刻t的值除了依赖于t之外,还与过程在这时刻的点数N(t)有关,则得到的是非齐次纯生过程。现在,若进一步假设过程在任一时刻t的强度除了依赖于t和N(t)之外,还可能与在时刻t前发生的N(t)个点的位置有关,换句话说,依赖于过程在时刻t之前(包含t)的全部历史,于是就得到更广泛一类的点过程——自激点过程。
基本介绍
- 中文名:自激点过程
- 外文名:self-exciting point process
- 所属学科:数学
- 所属问题:随机过程
- 相关概念:计数过程、样本分布、联合分布等
自激点过程的定义
在数学上,自激点过程被定义为满足下述条件的计数过程 :对任意实数
:对任意实数 和
和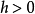 ,
,


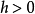
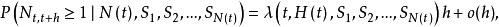



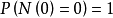
注意自激点过程的强度λ不仅随时间t变化,而且还是过程 的现实ω的函式,即强度本身是一随机过程,但它受点过程自身的演化制约。
的现实ω的函式,即强度本身是一随机过程,但它受点过程自身的演化制约。

如果计数过程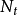 满足:
满足: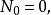 且对于小时间h有
且对于小时间h有
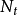
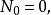

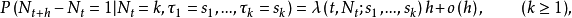
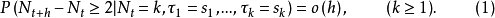
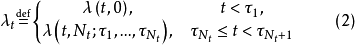
自激点过程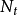 称为m-记忆的,如果
称为m-记忆的,如果
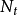
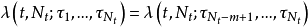
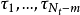
最简单的是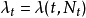 的情形,这是无记忆(0-记忆)的自激点过程情形,即下面的定义。
的情形,这是无记忆(0-记忆)的自激点过程情形,即下面的定义。
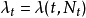
定义1计数过程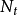 称为无记忆的自激点过程,如果
称为无记忆的自激点过程,如果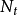 满足:
满足: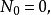 且存在正值函式
且存在正值函式 使对于小的h有
使对于小的h有
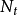
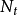
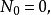


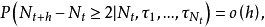
例1年龄 的
的 个人的群体在时刻
个人的群体在时刻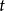 以前的死亡人数(死亡计数过程)
以前的死亡人数(死亡计数过程)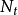 可以用无记忆的自激点过程建模,其强度过程为
可以用无记忆的自激点过程建模,其强度过程为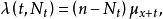 其中
其中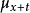 是年龄为
是年龄为 的死亡率,
的死亡率,


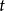
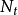
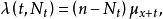
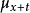

无记忆的自激点过程的有限维分布
无记忆的自激点过程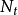 在有限个时刻上的联合分布为: 对于
在有限个时刻上的联合分布为: 对于 整数
整数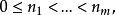
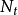

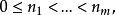
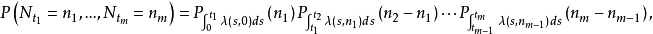
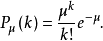
自激点过程的条件强度过程
定义2

于是,对于自激点过程有
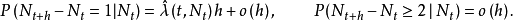
自激点过程的绝对机率
仿照初等机率论中Poisson过程的绝对机率的推导,可以得到
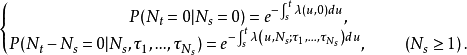
命题1 自激点过程的绝对机率满足如下的(常微分方程组)