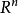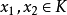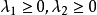设 C 为 中的凸集。C 的闸锥指所有满足如下条件 的全体：存在 ，对所有 ，均有 。

闸锥是实线性空间的集合的极集所生成的锥。设 A 为巴拿赫空间 X 的集合，X^*为 X 的对偶，那幺 A 的闸锥可表示为。

因此，闸锥就是 A 的支撑函式的有效域。当集合是包含原点的闭凸集时，闸锥就是回收锥的对偶锥。反之，如果回收锥的内部非空，那幺它也是闸锥的对偶锥。

在凸几何中，凸集(convex set)是在凸组合下闭合的仿射空间的子集。更具体地说，在欧氏空间中，凸集是对于集合内的每一对点，连线该对点的直线段上的每个点也在该集合内。例如，立方体是凸集，但是任何中空的或具有凹痕的例如月牙形都不是凸集。

特别的，凸集，实数R上（或複数C上）的向量空间中，如果集合S中任两点的连线上的点都在S内，则称集合S为凸集。

一类特殊的凸集被称之为凸锥，它有极其重要的性质和套用。既是锥又是凸集的点集称之为凸锥。常见的凸锥包括：二维平面中的半射线、整个n维欧式空间等。凸锥中有一个重要的定理，凸锥分离定理。

设是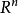中的点集，若点集既是锥又是凸集时，即当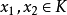时，对任意不同时为零的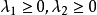，点，则称为凸锥。