博赫纳-里斯平均(Bochner-Riesz mean)是多重傅立叶级数一种重要的线性求和。
基本介绍
- 中文名:博赫纳-里斯平均
- 外文名:Bochner-Riesz mean
- 适用範围:数理科学
简介
博赫纳-里斯平均是多重傅立叶级数一种重要的线性求和。
设f∈L(Tn),f的傅立叶级数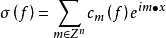 的α阶博赫纳-里斯平均是三角多项式
的α阶博赫纳-里斯平均是三角多项式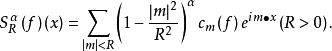
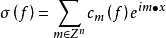
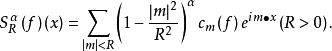
性质
阶数α可以是任意複数,它的临界阶是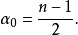
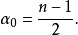
临界阶的意义在于:当α=α0时,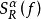 可类比于一元的傅立叶和。
可类比于一元的傅立叶和。
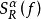
套用
博赫纳-里斯平均在多重傅立叶级数理论中是研究得较多的一种“球形”方式的线性平均。这里和式的格子点m是在球内{m||m|<R}取的。
傅立叶级数的线性求和
傅立叶级数的线性求和是用线性运算元对傅立叶级数的求和法。
从已给的傅立叶级数出发,构造新的三角级数或三角多项式,使之与所给的函式之间保持着线性的对应关係,这种构造新三角级数或三角多项式的方法称为傅立叶级数的线性求和法。
