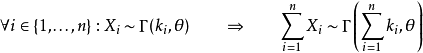在机率论中，任何随机变数的特徵函式(缩写：ch.f,複数形式：ch.f's)完全定义了它的机率分布。
基本介绍
- 中文名：特徵函式
- 外文名：ch.f's
- 缩写：ch.f
- t：一个实数
- i：虚数单位
- E：期望值
- 外文名：Characteristic function
定义
在机率论中，任何随机变数的特徵函式(缩写：ch.f,複数形式：ch.f's)完全定义了它的机率分布。在实直线上，它由以下公式给出，其中X是任何具有该分布的随机变数：
其中t是一个实数，i是虚数单位，E表示期望值。
用矩母函式MX（t）来表示（如果它存在），特徵函式就是iX的矩母函式，或X在虚数轴上求得的矩母函式。
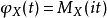
与矩母函式不同，特徵函式总是存在。
如果FX是累积分布函式，那幺特徵函式由黎曼-斯蒂尔切斯积分给出：
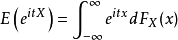
如果随机变数的机率密度函式存在，机率密度函式为，上述积分可以简化为：
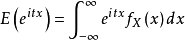
其中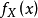
是随机变数X的机率密度函式。
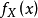
如果X是一个向量值随机变数，我们便取自变数t为向量，tX为数量积。
性质
特徵函式具有以下基本性质：
勒维连续定理
如果两个随机变数具有相同的特徵函式，那幺它们具有相同的机率分布； 反之， 如果两个随机变数具有相同的机率分布， 它们的特徵函式也相同(显然)。
独立随机变数和的特徵函式等于每个随机变数特徵函式的乘积。
反演定理
在累积机率分布函式与特徵函式之间存在双射。也就是说，两个不同的机率分布不能有相同的特徵函式。
给定一个特徵函式φ，可以用以下公式求得对应的累积机率分布函式F：
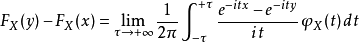
一般地，这是一个广义积分；被积分的函式可能只是条件可积而不是勒贝格可积的，也就是说，它的绝对值的积分可能是无穷大。
博赫纳-辛钦定理/公理化定义
任意一个函式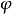
是对应于某个机率律
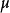的特徵函式，若且唯若满足以下三个条件：
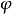
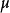
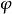
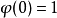
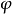
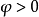
计算性质
特徵函式对于处理
特徵函式对于处理独立随机变数的函式特别有用。例如，如果X1、X2、……、Xn是一个独立（不一定同分布）的随机变数的序列，且
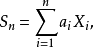
其中ai是常数，那幺Sn的特徵函式为：
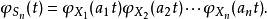
特别地，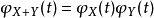
。这是因为：
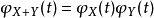
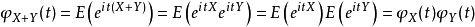
注意我们需要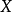
和
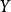的独立性来确立第三和第四个表达式的相等性。
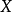
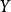
另外一个特殊情况，是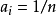
且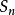
为样本平均值。在这个情况下，用
表示平均值，我们便有：
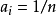
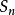
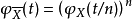
特徵函式的套用
由于连续定理，特徵函式被用于中心极限定理的最常见的证明中。
矩
特徵函式还可以用来求出某个随机变数的矩。只要第n个矩存在，特徵函式就可以微分n次，得到：
例如，假设X具有标準柯西分布。那幺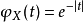
。它在 t=0处不可微，说明柯西分布没有期望值。另外，注意到
个独立的观测的样本平均值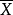
具有特徵函式
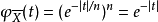，利用前一节的结果。这就是标準柯西分布的特徵函式；因此，样本平均值与总体本身具有相同的分布。
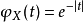
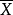
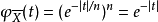
特徵函式的对数是一个累积量母函式，它对于求出累积量是十分有用的；注意有时定义累积量母函式为矩母函式的对数，而把特徵函式的对数称为第二累积量母函式。
一个例子
具有尺度参数θ和形状参数k的伽玛分布的特徵函式为：
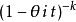
现在假设我们有：
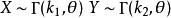
其中X和Y相互独立，我们想要知道X+Y的分布是什幺。X和Y特徵函式分别为：
根据独立性和特徵函式的基本性质，可得：
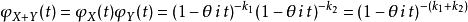
这就是尺度参数为θ、形状参数为k1+k2的伽玛分布的特徵函式，因此我们得出结论：
这个结果可以推广到n个独立、具有相同尺度参数的伽玛随机变数：
