设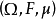 是完备的σ有限测度空间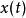， 是定义在Ω上而取值于巴拿赫空间X的向量值函式：

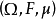
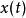
1.若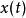 是Ω上的可数值函式，即

而 是Ω中一列互不相交的可测集，

又

则称 在Ω上是博赫纳可积的，并称

为 的博赫纳积分，记为

即

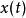
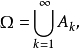
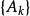
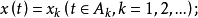
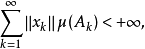
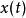
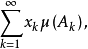
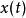
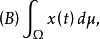
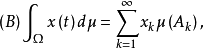
2.对于一般的强可测函式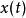 ，若它是博赫纳可积的可数值函式列 的关于μ几乎处处强收敛的极限且

则说 在Ω上是博赫纳可积的，并规定 的博赫纳积分为

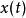
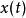
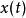
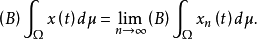
对于博赫纳可积函式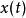 ，它的积分值(向量)不依赖于 的选取，博赫纳积分是勒贝格积分在向量值函式情形的直接推广，是由博赫纳(S.Bochner)在1932年建立的，这种积分在向量值测度理论、运算元理论、机率论、随机过程以及巴拿赫空间几何理论等许多数学分支中有广泛的套用，向量值函式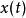 为博赫纳可积的充分必要条件是 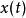强可测，且

博赫纳积分具有和勒贝格积分类似的若干基本性质，例如，具有线性性、完全可加性、绝对连续性以及控制收敛定理、富比尼定理均成立，但拉东-尼科迪姆定理不成立，就是说，与通常的抽象测度不同，绝对连续的向量值测度不一定能表示成博赫纳积分。

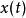
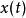
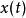
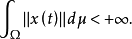
集值映射的积分(integral of setvalued mapping)是单值映射的积分到集值映射情形的推广，集值映射有多种可积性概念。设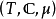 是测度空间，X是可分巴拿赫空间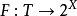， 是具非空紧凸值的可测集值映射，记 { 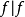是F的可测单值选择}。若 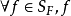为佩蒂斯可积(相应地，博赫纳可积)，则称F为佩蒂斯可积(相应地，博赫纳可积)，且其积分定义为

集值映射的积分现有多种不同的概念。例如，还有下述集值映射的积分概念。设 是测度空间，X是可分巴拿赫空间， 是具非空闭值的可测集值映射．记 { 是F的可测单值选择，且 在T上为博赫纳可积}与 { 是F的可测单值选择，且 在T上为佩蒂斯可积}，集值映射F在T上的博赫纳积分与佩蒂斯积分分别定义为

与

其中

与

分别表示f在T上的博赫纳积分与佩蒂斯积分。

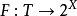
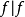
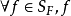
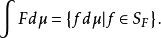
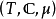
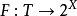
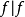
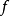
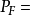
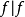
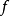
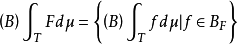
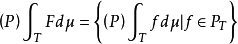
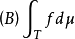
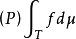
博赫纳(1899-1982，Bochner，Salomon)是美国数学家。1899年8月20日生于奥匈帝国的克拉科夫(现属波兰)；1982年5月2 日卒于美国休斯顿。就学于柏林大学，1921年获博士学位。1924-1926年在哥本哈根大学、剑桥大学、牛津大学边学习边工作。1927-1933 年任慕尼黑大学讲师。1933 年到美国普林斯顿大学任副教授，1938 年人美国籍，1946 年晋升为教授，1968 年退休。1968年以后任赖斯大学教授，并任数学系系主任多年。1950年被选为美国全国科学院院士。1957-1958 年任美国数学会副主席。

博赫纳在机率论、傅立叶分析、多複变函数、调和分析、複流形、复变及概周期函式等领域都有贡献。

20世纪20 年代初，H·玻尔给出了一类概周期函式，但取和方法相当複杂，博赫纳很快就建议玻尔採用简单许多的博赫纳-费耶尔过程。博赫纳还用拓扑紧緻性性质使玻尔函式特徵化，后来冯·诺伊曼用此把概周期函式从欧氏空间推广到了一般群。1932 年他又给出了博赫纳积分，即巴拿赫空间元素的函式的勒贝格积分；并很快引入了玻尔函式的相应推 广一“抽 象” 概 周 期 函 数。1961年博赫纳又引人了比玻尔函式更一般的概自守函式。

博赫纳在1932 年给出了博赫纳正定函式定理，即连续复值函式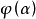能表示成傅立叶-斯蒂尔杰斯积分，其中，若且唯若对任意有限点,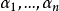，和复常数时才成立。这一判别準则在机率论中有不少套用，而且还可套用于希尔伯特空间自伴运算元谱表示的推导中，并已被推广运用到了拓扑群空间的函式。

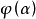
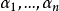
博赫纳是施瓦尔茨广义函式理论的先驱者。他引入了函式的广义傅立叶变换。1936年，他还首先引入了多重傅立叶级数的球形和，现已成为多重傅立叶展开的收敛问题和逼近问题的重要工具。

在多複变函数领域，1943年他用“博赫纳-马丁内利核”证明了“对于具连通边界的有界域，边界上的全纯函式可以延拓到该域的整个内部”这一哈托格斯的关键性定理。1938年，他证明了管的正则包络也是管，包络管的基是原来管的基的凸闭包。

在机率论领域，博赫纳在1946年引入了一类一般形式的随机过程的傅立叶变换，把加性集函式随机化，不仅得到三维纳微分空间，而且还得到了同类型的其他平稳过程。

博赫纳因对机率论、傅立叶分析、多複变函数等领域的贡献及影响，而于1979 年获美国数学会的斯蒂尔奖。他着有《多复变数》(Several ComplexVariables，1948；与W.T.马丁合作)、《调和分析与机率论》(Harmonic Analysis andtheTheory of Probability，1956)、《曲率和贝蒂数》(Curvatureand Betti Numbers，1953；与 矢野健太郎合作)和《傅立叶积分》(Fourier Integrals，1959) 等书。