半鞅（Semimartingale）是机率论的概念。若一随机过程为一局部鞅和一适应的有界变差过程之和，则称该随机过程为一半鞅。半鞅的概念包含了众多常用的随机过程，扩充了伊藤积分的定义範围，从这个意义上说，半鞅是鞅和局部鞅的扩展。
基本介绍
- 中文名：半鞅
- 外文名：Semimartingale
- 领域：数学
- 适用领域：机率论
定义
概述
一个定义在带域流的机率空间（Ω
）的实值随机过程X被称为半鞅，若X有如下分解：
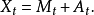
右连左极函式
在数学中，右连左极函式（càdlàg，RCLL）是指定义在实数集或其子集上的处处右连续且有左极限的函式。这类函式在研究有跳跃甚至是需要跳跃的随机过程时很重要，这类随机过程不像布朗运动具有连续的样本轨道。给定定义域上的右连左极函式的集合称为斯科罗霍德空间（Skorokhod space）。全部连续函式都是右连左极函式。由累积分布函式的定义知所有的累积分布函式都是右连左极函式。
性质
- 多个半鞅的线性组合仍然是半鞅。
- 多个半鞅的积仍然是半鞅。
- 任意半鞅的二次变差都存在。
- 若X为一半鞅，f为二次连续可微函式，则f(X)也是半鞅。
例子
- 凡是右连左极鞅都是半鞅，更一般地，上鞅和下鞅也都是半鞅。
- 布朗运动是连续鞅，因此也是半鞅。
- 适应并连续可微过程是有界变差过程，因此也是半鞅。
- 莱维过程并不一定都是鞅，但一定都是半鞅。
布朗运动
布朗运动（Brownian motion）过程是一种常态分配的独立增量连续随机过程。它是随机分析中基本概念之一。其基本性质为：布朗运动W(t)是期望为0、方差为t（时间）的正态随机变数。对于任意的r小于等于s，W(t)-W(s)独立于的W(r)，且是期望为0、方差为t-s的正态随机变数。可以证明布朗运动是马尔可夫过程、鞅过程和伊藤过程。
它是在公元1827年英国植物学家罗伯特·布朗利用一般的显微镜观察悬浮于水中由花粉所迸裂出之微粒时，发现微粒会呈现不规则状的运动，因而称它布朗运动。布朗运动也能测量原子的大小，因为就是有水中的水分子对微粒的碰撞产生的，而不规则的碰撞越明显，就是原子越大，因此根据布朗运动，定义原子的直径为10-8厘米。
莱维过程
莱维过程（Lévy process）源于法国数学家保罗·皮埃尔·莱维，是连续时间上的一种拥有独立稳定增量的左极限右连续（Càdlàg）的随机过程。着名的例子有Wiener过程和泊松过程。
参见
- 鞅
- 局部鞅
- 布朗运动