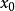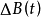伊藤积分((Ito integral)是一种随机积分,它是由日本数学家伊藤清首先提出和研究的。伊藤方程的重要性之一在于它的解过程是一个马氏过程,从而可以把马氏过程的许多深入结果利用上。
基本介绍
- 中文名:伊藤积分
- 外文名:Ito stochastic integral
- 定义:一种随机积分
- 套用学科:数学术语
- 範畴:数理科学
- 涉及:伊藤
概念
在统计物理中的郎之万方程,应该是随机微分方程,而且不是普通意义下的随机微分方程
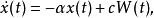
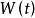
更一般地,考虑方程
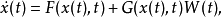
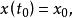

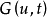
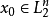
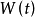

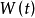
注意到白噪音过程是作为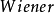 过程的导过层是引入的,因而上式在形式上等价于方程
过程的导过层是引入的,因而上式在形式上等价于方程
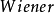
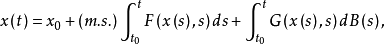
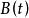
上式比较容易赋以严格的定义,只须对其右端第二个积分加以解释罢了。我们可以把第二个积分理解为斯蒂尔吉斯均方积分
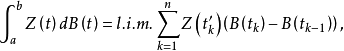

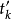
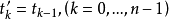
基本原理
定义:设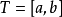 ,
,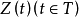 是随机过程,对
是随机过程,对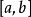 区间取一划分
区间取一划分
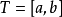
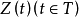
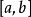
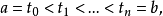
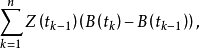
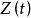

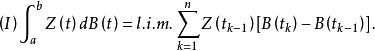
定理:若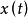 在
在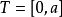 上连续,对任意
上连续,对任意 ,都有
,都有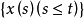 与
与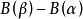 独立,则
独立,则
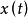
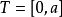

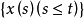
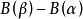
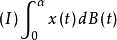
定理:设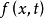 与
与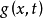 是两个实函式,满足
是两个实函式,满足
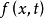
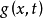
(1)都在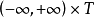 上连续,且对每一
上连续,且对每一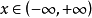 ,关于
,关于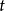 一致连续。
一致连续。
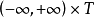
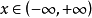
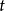
(2)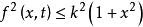 ,
,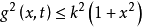 ,其中
,其中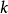 为一常数。
为一常数。
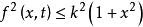
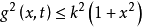
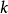
(3)李普西兹条件: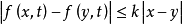 ,
,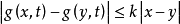 ,又设
,又设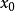 与任意
与任意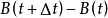 独立,则伊藤方程有唯一确定的解。
独立,则伊藤方程有唯一确定的解。
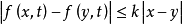
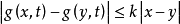
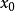
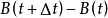
定理:设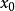 与任意
与任意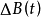 独立,则伊藤方程的解是一个马尔科夫过程。
独立,则伊藤方程的解是一个马尔科夫过程。