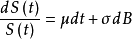伊藤过程可看成为一般化的维纳过程,它直接把布朗运动理解为随机干扰,从而赋予了布朗运动最一般的意义。
基本介绍
- 中文名:伊藤过程
- 外文名:Itô process
- 表达式:dx(t)=μ(t,x)dt+σ(t,x)dz
- 提出者:维纳
- 提出时间:1923
- 套用学科:数学
- 适用领域範围:数学,工程学,经济学等
简介
随机微分方程(SDE)形如
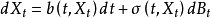
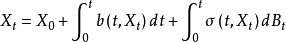
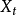
令
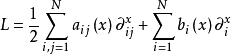
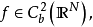
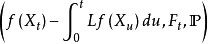
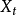
背景
控制论的发明人维纳在1923年指出,布朗运动在数学上是一个随机过程,提出了用“随机微分方程”来描述,因此人们也把布朗运动称为维纳过程。
日本数学家伊藤发展建立了带有布朗运动干扰项的随机微分方程,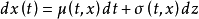 ,其中,σ(t,x)是干扰强度,μ(t,x)是漂移率,σ(t,x)dz服从常态分配N(0,σ2(t,x))。
,其中,σ(t,x)是干扰强度,μ(t,x)是漂移率,σ(t,x)dz服从常态分配N(0,σ2(t,x))。
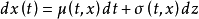
该方程描写的过程是伊藤过程。伊藤过程可看成为一般化的维纳过程,它直接把布朗运动理解为随机干扰,从而赋予了布朗运动最一般的意义。
布朗运动
布朗运动是随机涨落的典型现象,一般地说,许许多多的巨观观测,都要受到布朗运动的限制。法国经济学家Bachelier L把股价的变动理想化为布朗运动.
在此基础上,经济学家把伊藤过程方程用于描写股票价格行为过程的一种模式,为更确切地描写股票价格的行为过程(只限于在短时间内),伊藤过程方程被修正为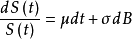 。其中σ为股票价格波动率、 μ为股票价格的预期收益率,人们把它称为股价方程,它是一个随机微分方程。由伊藤过程描述的股价方程是一个正向的随机微分方程,从确定的S(0)=S0出发,根据布朗运动的随机变数B(t)在0-t之间的形态,来推断轨线的统计行为。
。其中σ为股票价格波动率、 μ为股票价格的预期收益率,人们把它称为股价方程,它是一个随机微分方程。由伊藤过程描述的股价方程是一个正向的随机微分方程,从确定的S(0)=S0出发,根据布朗运动的随机变数B(t)在0-t之间的形态,来推断轨线的统计行为。