鞍结分岔(saddle-node bifurcation)一种分岔类型,指控制参数变化过程中系统因形成鞍结点而出现的分岔。
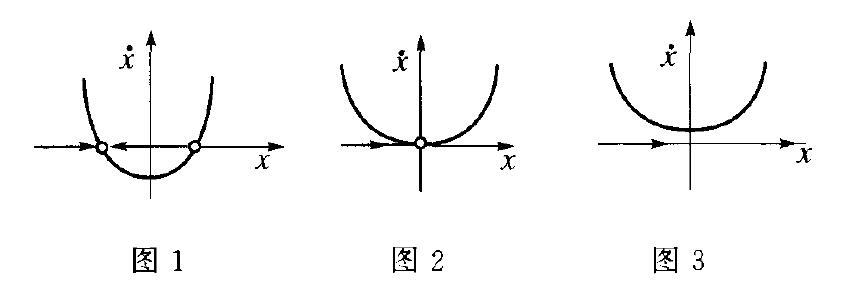
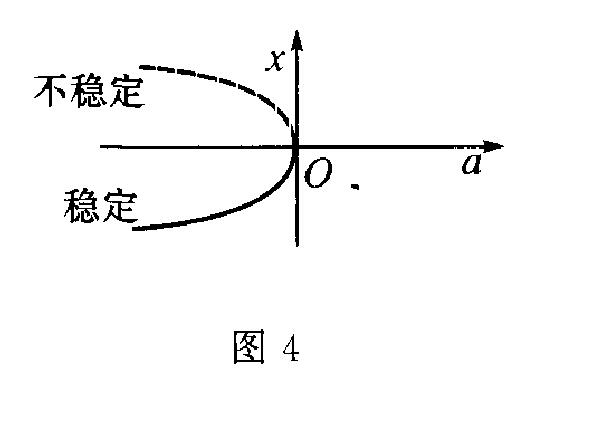
鞍结分岔(saddle-node bifurcation)一种分岔类型,指控制参数变化过程中系统因形成鞍结点而出现的分岔。以一阶系统x·=a+x2为例,控制参数a可取任何实数:a>0时不动点方程a+x2=0没有实数解,表示系统没有定态(图3);a<0时方程有两个实数解:x1,2= ,左侧为稳定定态点,右侧则为不稳定定态点(图1);图2所示分岔点a=0处不动点x=0是半稳定的,称为鞍结点。从而在平面中用几何方法可方便地找到不动点并判别稳定性。总之,当控制参数a由正值逐步减小而跨越鞍结点时,将出现定态点的创生,反方向变化则出现定态点的消失,都表示系统的分岔行为。这种分岔的特点亦可用图4表示。
,左侧为稳定定态点,右侧则为不稳定定态点(图1);图2所示分岔点a=0处不动点x=0是半稳定的,称为鞍结点。从而在平面中用几何方法可方便地找到不动点并判别稳定性。总之,当控制参数a由正值逐步减小而跨越鞍结点时,将出现定态点的创生,反方向变化则出现定态点的消失,都表示系统的分岔行为。这种分岔的特点亦可用图4表示。