流体格线法(fluid-in-cell method)是求解非定常可压缩流动问题的一种欧拉差分法。欧美简称它为FLIC法，苏联称它为大粒子法。

流体格线法是里奇(Rich , M.)于1963年，金特里(Gentry, R. A. )、马丁(Martin, R. E. )、戴利<Daly, B. J.)于1966年以及别洛柴可夫斯基(EenouepxoBCxH,O. M.)、达维多夫(}OBbIj[OB, }. N1.)于1971年在哈洛的质点格线法基础上将单一格线元看做一个大粒子而发展起来的。

它和PIC法不同之处在于在第二步计算中不计算质点的迁移，而计算连续流体的迁移，即先算出通过格线边界的质量输运量，从而得到每个格线的新密度，再算出通过格线的质量所携带的动量和能量的输运量，最后得到每个格线的新速度和能量。该方法的突出特点是对于複杂的流动问题用比较适中的计算机时间就可得到相当準确的解。它特别适于包含大流动畸变的单种物质的流动问题。

在边界是 r 的任意区域D中、无粘性、无热传导的流体动力学方程组可写成

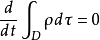
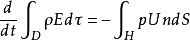
其中ρ是流体的密度，U是流体速度，E是总能量，它是比内能 e和动能之和，

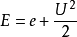
τ是体积元（或面元），s是面积元 （或线元）， n是边界τ上外法线的单位向量。第一个方程表示质量守恆，第二个方程表示动量变化率等于边界上压力和，第三个方程表示总能量的变化率是外来作功之和 .
另一方面，可以推出，

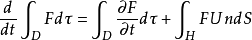
这里F=（ρ，ρu，ρv，ρE），此方程右端第一项表示在固定区域中质量、动量和总能量的变化率，第二项分 别是单位时间内流体经边界流过的质量流、动量流和能量流。

前三个方程是拉格朗日方程组。将其带入方程4可以得到欧拉流体动力学方程组。

流体格线法是以欧拉方程组作为 第一步，而以欧拉流体动力学方程组作为第二步来求欧拉 方程组的数值解 ：先用已算好的时刻tⁿ的结果作为初值连同边界条件一起求逼近欧拉方程组的数值积分，这一步只考虑了与压力有关的项，而后，以这一 步所得到的中间结果作为 初值，连同边界条件一起，求逼近欧拉流体动力学方程组数值 积分，该步考虑了对流项的贡献。这样就得到了逼近方程的数值解。

质点格线法（particle-in-cell method）是计算二维非定常可压缩理想流动问题的欧拉－拉格朗日混合方法,简称PIC法，它特别适用于计算具有多种介质和大变形流动的问题。

在流体动力学中，通常可用欧拉和拉格朗日两种不同坐标系来求解流体动力学问题，即所谓欧拉法和拉格朗日法。欧拉法可用于求解流体大畸变问题，但精度不高，而且在各个区域进行物质输运时会产生严重的物质扩散，使界面和自由面的位置不能精确确定。拉格朗日法正好相反，计算精度较高，能精确确定界面和自由面，但不能处理流体大畸变和在各种介质之间有剪下间断的滑移现象。针对这种情况，美国F.H.哈洛等人于1955年成功地把欧拉法和拉格朗日法结合起来，提出了质点格线法。

PIC法的基本要点是，把含有多种介质的流动所通过的区域用欧拉法分成有限个格线，每个格线中的每种流体，用一组特定的离散化拉格朗日质点表示。图中“×”表示一种流体质点,“·”表示另一种流体质点。只包含一种流体质点的格子称为纯单元，两种流体质点同时存在的格子称为混合单元，不存在任何流体质点的格子称为空单元。每个质点具有一定的质量，每个格线单元内的质点数目和质点分布都以流体流动的初始状态为依据，而且这些质点具有一定的速度和能量。计算开始后,质点在欧拉格线之间迁移,表示流体在运动。

在每个时间步长内，计算分两步：第一步用欧拉法计算，即忽略偏微分方程中的输运效应，用差分方法计算由压力分布所引起的欧拉格线上速度（或动量）和能量的变化。若一个格线内含有多种流体，就应按一定的规则把能量的改变数适当分配给不同的质点。第二步是质点迁移计算，它是在第一步的基础上，按一定的加权平均方法计算出每个质点的速度和在时间步长结束时的新位置。一个质点从一个格线迁移到另一个格线，就把所携带的质量以及相应的动量和能量从原来的格线输送到新的格线中去。这一步实质上是对第一步计算中忽略的输运效应计算的补偿。

在具有激波间断的流动中，处理激波间断是一个难题（见激波数值处理）。PIC法由于有非线性的耗散效应，不仅可以减少差分格式所引起的起伏现象，而且起着类似于人工粘性的作用。因此，PIC法能自动处理流动中的激波间断。但在低速流动和固壁条件的计算中，这个耗散效应很弱，为了使计算稳定，还须引入人工粘性。

要得到较好的计算结果，除应考虑满足一定的稳定性条件外，还须考虑每个单元内的质点数目和分布以及它们的内能等。