阶梯型矩阵是矩阵的一种类型。它的基本特徵是如果所给矩阵为阶梯型矩阵则矩阵中每一行的第一个不为零的元素的左边及其所在列以下全为零。
基本介绍
- 中文名:阶梯型矩阵
- 外文名:Row-Echelon Matrix
- 类型:模型
- 条件:需满足两个条件
- 用途:计算
简介
一个矩阵成为阶梯型矩阵,需满足两个条件:
(1)如果它既有零行,又有非零行,则零行在下,非零行在上。
(2)如果它有非零行,则每个非零行的第一个非零元素所在列号自上而下严格单调上升。
阶梯型矩阵的基本特徵:
如果所给矩阵为阶梯型矩阵则矩阵中每一行的第一个不为零的元素的左边及其所在列以下全为零。
画法
 画法1
画法1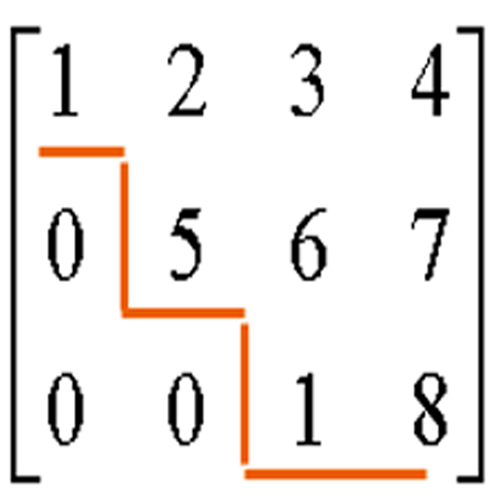 画法2
画法2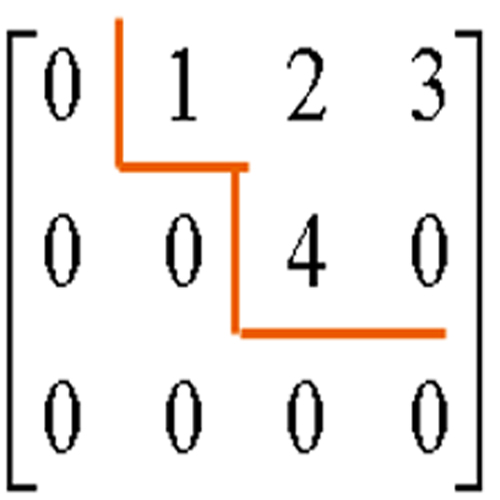 画法3
画法3上面的三种阶梯矩阵的画法。
图二、图三的最后一列可看为方程的值列。
