初等矩阵是指由单位矩阵经过一次三种矩阵初等变换得到的矩阵。初等矩阵的模样可以写一个3阶或者4阶的单位矩阵。
首先:初等矩阵都可逆,其次,初等矩阵的逆矩阵其实是一个同类型的初等矩阵(可看作逆变换)。例如,交换矩阵中某两行(列)的位置;用一个非零常数k乘以矩阵的某一行(列);将矩阵的某一行(列)乘以常数k后加到另一行(列)上去。若某初等矩阵左乘矩阵A,则初等矩阵会将原先施加到单位矩阵E上的变换,按照同种形式施加到矩阵A之上。或者说,想对矩阵A做变换,但是不是直接对矩阵A去做处理,而是通过一种间接方式去实现。
基本介绍
- 中文名:初等矩阵
- 外文名:Elementary matrix
- 所属学科:线性代数
- 相关名词:单位矩阵
- 套用领域:数学
- 别称:基本矩阵
概念
初等变换有三种
(1)交换矩阵中某两行(列)的位置;
(2)用一个非零常数k乘以矩阵的某一行(列);
(3)将矩阵的某一行(列)乘以常数k后加到另一行(列)上去。
三类初等矩阵都是可逆矩阵,即非奇异阵。
三类初等矩阵行列式的值是:
(1):-1
(2):k
(3):1
性质
1、单位矩阵第i,j两行互换得到的方阵为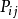 ,将矩阵
,将矩阵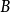 的第i,j两行互换所得矩阵
的第i,j两行互换所得矩阵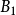 ,即有
,即有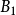 =
=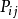 *
*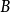 。
。
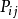
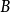
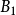
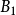
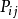
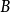
说明:任意矩阵 的交换i,j行(列),取决于
的交换i,j行(列),取决于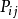 是左乘
是左乘 ,还是右乘
,还是右乘 ,即:
,即: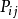 *
* 是交换行i,j变换,
是交换行i,j变换, *
*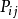 是交换列i,j变换。
是交换列i,j变换。

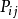


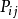


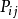
2、单位矩阵第i行乘以常数k得到初等方阵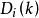 ,将矩阵
,将矩阵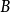 的第i行乘以k得到矩阵
的第i行乘以k得到矩阵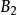 ,即有
,即有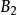 =
=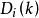 *
*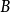 。
。
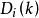
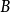
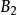
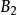
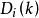
说明:任意矩阵 的行(列)乘以常数k,取决于
的行(列)乘以常数k,取决于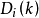 是左乘
是左乘 ,还是右乘
,还是右乘 ,即 :
,即 :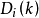 *
* 是矩阵
是矩阵 行乘以常数k变换,
行乘以常数k变换, *
*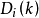 是矩阵
是矩阵 列乘以常数k变换。
列乘以常数k变换。

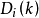


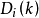



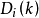

3、将单位矩阵的第i行的k倍加到第j行得到初等方阵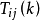 ,矩阵
,矩阵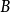 的第i行的k倍加到第j行得到矩阵
的第i行的k倍加到第j行得到矩阵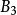 ,即有
,即有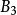 =
=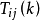 *
*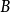 ;将单位矩阵的第j列的k倍加到第i列得到初等方阵
;将单位矩阵的第j列的k倍加到第i列得到初等方阵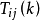 ,矩阵
,矩阵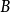 的第j列的k倍加到第i列得到矩阵
的第j列的k倍加到第i列得到矩阵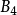 ,即有
,即有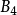 =
=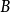 *
*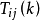 。
。
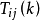
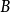
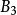
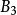
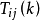
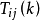
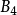
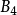
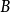
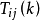
说明:任意矩阵 与初等矩阵相乘,表示对A进行初等变换,但对A进行的是行初等变换还是列变换,取决于初等矩阵
与初等矩阵相乘,表示对A进行初等变换,但对A进行的是行初等变换还是列变换,取决于初等矩阵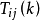 是左乘
是左乘 ,还是右乘
,还是右乘 ,即:
,即: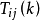 *
* 是行初等变换,此时
是行初等变换,此时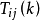 的变换表示将
的变换表示将 的第i行的k倍加到第j行(顺序从前向后);
的第i行的k倍加到第j行(顺序从前向后); *
*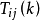 是列初等变换,此时
是列初等变换,此时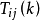 的变换表示将
的变换表示将 的第j列的k倍加到第i列(顺序从后向前)。
的第j列的k倍加到第i列(顺序从后向前)。

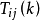


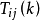

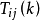


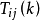
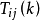

套用
(1)在解线性方程组中的套用
初等行变换不影响线性方程组的解,也可用于高斯消元法,用于逐渐将係数矩阵化为标準形。初等行变换不改变矩阵的核(故不改变解集),但改变了矩阵的像。反过来,初等列变换没有改变像却改变了核。
(2)用于求解一个矩阵的逆矩阵
有的时候,当矩阵的阶数比较高的时候,使用其行列式的值和伴随矩阵求解其逆矩阵会产生较大的计算量。这时,通常使用将原矩阵和相同行数(也等于列数)的单位矩阵并排,再使用初等变换的方法将这个并排矩阵的左边化为单位矩阵,这时,右边的矩阵即为原矩阵的逆矩阵。

