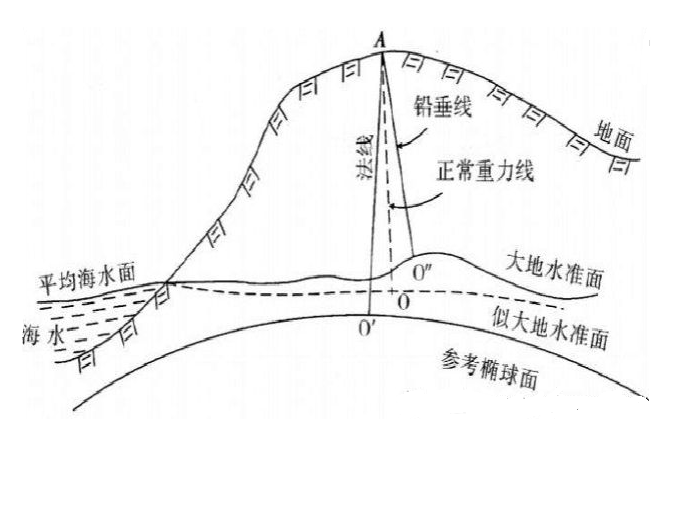
天文重力水準(astro-gravimetric leveling)是利用天文大地垂线偏差和重力测量数据,推算相邻两点的大地水準面差距之差(高差或高程异常差)的方法。当两天文点的距离较远,垂线偏差非线性变化时,须利用重力测量数据算出垂线偏差非线性变化的影响,才能较精确的推算出天文大地水準面差距之差。
基本介绍
- 中文名:天文重力水準
- 外文名:astro-gravimetric leveling
- 作用:推算相邻点的大地水準面高差
- 数据来源:天文大地垂线偏差和重力测量数据
- 一级学科:工程技术
- 二级学科:测绘科学
发展历史
苏联的天文重力水準工作开始于上世纪三十年代,即莫洛金斯基提出这个方法之后。利用苏联摆仪全盘重力测量资料按天文重力水準方法求得的似大地水準面高度,曾用于推求克拉索夫斯基椭球的最适合的大地测量起始数据,以后在苏联天文大地网的整体平差中又用来归算观测值。
卫国战争之后,天文重力水準工作获得了新的发展。莫洛金斯基证明;为了满足似大地水準面相对于克拉索夫斯基椭球之高度的要求,必须提高精度,即似大地水準面高度的均方误差不得大于±3米。根据他的建议开始布设许多精度较高的天文重力水準。以此作为天文大地网中将似大地水準面高度逐步传递到基线网的干线。在这些路线上每隔70~100公里测定一个天文点,其周围半径约50公里範围内根据专门的方案进行加密重力测量,起先是用弹性摆加密,后来用重力仪加密。根据地形的特徵和重力场的複杂程度,以不同的密度进行加密测量,并保证重力垂线偏差分量计算的均方误差能够达到0.4″~0.5″。
在上世纪五十年代末期,苏联领土上为勘查矿产而进行的详细重力测量得到广泛发展。这些测量已保证重力垂线偏差的计算精度达0.45″,许多地区高于0.3″。因此,在大多数情况下有可能在天文测定的正常密度为100公里(最大为200公里)的基础上,用纯室内计算的方法建立具有足够精度的天文重力水準路线。天文重力水準路线的布设是这样的:它儘可能通过已经进行了大量重力测量的地区,而附加的工作只限于测定有限数量的天文点,以及在少数情况下只在半径不大的範围内进行加密重力测量。
随着地球物理重力勘探工作的发展,利用室内计算方法建立了大量新的天文重力水準路线。几乎所有的天文重力水準路线闭合环变成了周长自1000到4000公里的闭合环。在设计天文重力水準路线时,力求达到天文重力水準的每公里线路先验误差达3厘米/√(公里)。个别路线上所得值的範围为1.5~4.8厘米/√(公里)。
天文重力水準闭合环高差的平差採用与几何水準闭合环平差相同的方案进行。
对天文重力水準闭合环网上不同点的似大地水準面高度进行了相对于起始点普尔科伐的精度估计,它既顾及天文重力水準本身的误差,也顾及平面大地坐标误差的间接影响。在苏联的大部分领土上所得误差不超过2米,只在最边远地区误差达6米,其中主要是平面坐标误差的间接影响。
每个天文重力水準闭合环内的似大地水準面高度ζ是利用重力似大地水準面高度ζ'(计算的积分半径为1000或2000公里)进行内插的,所採用的公式为ζ=ζ'+(ζ-ζ')内插。
利用一定大小的梯形平均法耶异常在电子计算机上求得值ζ',在平原梯形的大小为(1°×1°),在山区为(10′×15′)。这一附加计算的误差不超过1.5米。因此,总的说来,似大地水準面高度的确定精度既高而又均匀,这对苏联天文大地网观测资料的归算是足够的。
计算
设图1,A、B为两个天文点,它们之间的相对坐标已由三角测量进行联繫。因此,它们的相对垂线偏差时可以按天文和大地测量的坐标差来推算的。但是,它们之间的距离较长。例如,我国的大地测量的锁环,一般是100~150公里长,有时达到200公里。我们只在锁环的交叉点上测有天文坐标。如果只用这样远的垂线偏差来推算大地水準面的相对高低,必然会导致错误的结果。因为,在这样远的距离之内,垂线随时在变化,有的地方大一些,而在另一个地方又小一些,甚至有些地方的变化方向是相反的,绝不可能是从一端均匀地变化到另一端。莫洛金斯基的天文重力水準就是利用重力数据在两个垂线偏差点之间进行内插。设图1中的A及B点上的垂线偏差为εa及εb。它们是在AB方向上的偏差,可以从所推算得到子午线及卯酉圈的偏差ξ,η按AB的方向换算而得。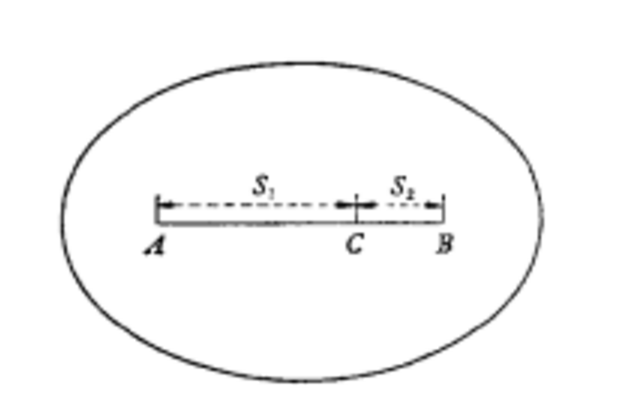 图1
图1
 图1
图1现在,假定用重力数据推算A及B两点的垂线偏差,数据只用到一定的範围,例如,图1中曲线所画的範围Σ。由于没有考虑到外部範围,即Σ区域以外的Σ',垂线偏差将具有一个误差,设为δεa,故準确的重力垂线偏差应等于
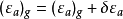
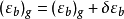
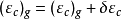
如果所用重力资料的範围是足够大的,则可以假定δεc是与离A点(或B点)的距离成比例的。现在,设C点离A及B点的距离各为S1及S2,则
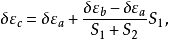
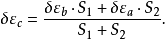
在另一方面,重力数据所推算的垂线偏差与从天文-大地测量所求得的垂线偏差也不会完全相同.因为,大地测量所推导出来的经纬度是根据一个所採用的参考椭球面推算的,并且也是根据某一个中心点的假定坐标出发的.而前者则接近于绝对值(假如重力资料是足够的,并且所依据的椭球面是真正的地球椭球面).但是,我们仍旧可以假定,在Σ计算範围之内,它们之间的差别与距离成比例.现在,假设εa,εb及εc为天文-大地测量的垂线偏差,则
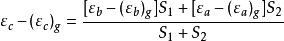
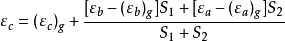
这就是垂线偏差的内插公式,在已经知道了A,B两点上的天文-大地测量垂线偏差εa及εb以及重力垂线偏差(εa)g,(εb)g的条件下,即可根据C点上的重力垂线偏差(εc)g以推算它的天文-大地测量垂线偏差εc。
全国天文、重力水準网的布设研研究
天文、重力水準是国家天文大地测量控制网建设中的重要研究课题。该课题所依据的理论是苏联学者莫洛金斯基提出来的,但由于我国地域大、地形複杂的特殊条件,在实际套用中遇到新的理论和技术问题。以方俊为首的研究小组从20世纪50年代中期开始,对此开展了广泛研究。
1957年,测量製图研究室与国家测绘总局重力队一起制订了平原和山区天文重力水準的“重力测量计画”,方俊提出了沿全国一等三角锁布设高精度和低精度两种天文、重力水準路线的实施方案。这一方案与苏联採用的密布法相比,在平原地区重力点的数目可减少40%,在山区可减少1/3。节省了人力、时间和经费。
1958~1961年,针对我国平原、山岳和山区的不同条件,许厚泽、李瑞浩、骆呜滓等建立了14000km2的鄂西北天文水準试验场,开展天文、重力水準布设与计算的试验研究。实验场内施测了9个三等天文点、253个重力点,完成了山岳地区天文水準和天文重力水準试验的计算任务,得出利用天文水準代替重力水準,既保证精度,又减少了工作量的结论。1958年,方俊在平原地区的天文、重力水準计算中提出了以平均重力异常为基础的方俊模板计算方法,将莫洛金斯基的椭圆一双曲线坐标模板改为直角坐标模板,使係数的计算大为简化,且精度优于前者。这一研究成果以《天文、重力水準的方俊模板》在《中国科学》上发表,很快引起国际上的重视,先后被编入苏联、东欧及我国的教科二阮称为“方俊模板计算法”,还被1960年莫洛金斯基的着作所引用。事隔20年后的1979年,方俊又设计了按单独天文点先行计算然后拼接的新方案,突破了将两个天文点合併计算的传统思想,避免了大量的重複计算,使计算工作量减少70%,且便于电脑程式的编制。在同一时期方俊还发表了《顾及扁率一次项的地球表面形状问题》一文,对扁率级斯托克斯问题提供了新的解法,丰富了大地重力学理论。
1961~1965年的主要研究工作有:
(1)许厚泽提出了维宁曼尼兹垂线偏差中函式最佳逼近问题的解法,改进了权威的莫洛金斯基逼近公式,建立了一种扁率级的高程异常和垂线偏差统一逼进模型理论;又在天文重力水準计算中提出了处理天文、重力水準的极圆坐标模板,因其计算简便、精度高,被国家测绘部门採用;在鄂西北山区高精度天文、重力水準试验网的数据处理中,结合山区地形複杂的实际情况,许厚泽还使用了空间重力异常的间接内插法,即现代广泛使用的移去恢复法。
(2)李瑞浩参与并组织了我国天文、重力水準网方案的制定和实施,建立青藏地区重力控制网;完成武昌原点的绝对垂线偏差实施方案的研究;还提出了鄂尔多斯地区代表误差和内插误差公式,确定了山区重力代表误差和内插误差的数值;利用球函式法研究我国重力场分布,构建了中国重力场球函式展式模型,解决了国际重力公式对中国的适应性问题;在天文、重力水準的计算中,解决了莫洛金斯基计算方法中极区非线性问题。
(3)骆鸣津发表了《用球函式解算重力测量的基本微分方程》,该文的主要结论为:在保持外空扰动位函式不变时,可将地面的扰动位解析延拓到球面上。这与国际着名地球物理学家贝亚哈马(Bjerhanmmar)同年发表的论文观点一致。