选票分配的基本原则是公平合理,要做到公平合理。一个简单的办法是,。但是会出现这样的问题:人数的比例常常不是整数。一个简单的办法是四捨五入,可四捨五入的结果可能会出现名额多余,或名额不足的情况。因为有这个缺点,美国乔治·华盛顿时代的财政部长亚历山大·汉密尔顿在1790年提出一个解决名额分配的办法,并于1792年为美国国会所通过。
基本介绍
- 中文名:阿拉巴马悖论
- 基本原则:公平合理
- 时间:1792年
- 原理:选票按人数比例分配
简介
美国国会的议员是按州分配。假定美国的人口数是p,各州的人口数分别是p1,p2,Λ,pl。再假定议员的总数是n,记:
称它为第i个州分配的份额.汉密尔顿方法的具体操作如下: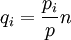
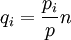
(1) 取各州份额qi的整数部分[qi],让第i个州先拥有[qi]个议员。
(2) 然后考虑各个qi的小数部分{qi},按从大到小的顺序将余下的名额分配给相应的州,直到名额分配完为止。
汉密尔顿方法看起来十分合理,但是仍存在问题。按照常规,假定各州的人口比例不变,议员名额的总数由于某种原因而增加的话,那幺各州的议员名额数或者不变,或者增加,至少不应该减少,可是汉密尔顿方法却不能满足这一常规。1880年,阿拉巴马州曾面临这种状况,人们把汉密尔顿方法产生的这一矛盾叫作阿拉巴马悖论。
这个问题从诞生之日起,就一直吸引着众多政治家和数学家去研究。这里要特别提出的是,1952年数学家阿罗证明了一个令人吃惊的定理——阿罗不可能定理,即不可能找到一个公平合理的选举系统。这就是说,只有相对合理,没有绝对合理。原来世上本无“公”!阿罗不可能定理是数学套用于社会科学的一个里程碑。
实例说明
假定某学院有三个系,总人数是200人,学生会需要选举20名委员,表1是按汉密尔顿方法进行分配的结果。
表1:
系别 | 人数 | 所占份额 | 应分配名额 | 最终分配名额 |
甲 | 103 | 51.5 | 10.3 | 10 |
乙 | 63 | 31.5 | 6.3 | 6 |
丙 | 34 | 17 | 3.4 | 4 |
合计 | 200 | 100 | 20 | 20 |
由于考虑到20个委员在表决提案时会出现10:10的结局,所以学生会决定增加1名委员。按照汉密尔顿方法分配名额得到表2。
表2:
系别 | 人数 | 所占份额 | 应分配名额 | 最终分配名额 |
甲 | 103 | 51.5 | 10.815 | 11 |
乙 | 63 | 31.5 | 6.615 | 7 |
丙 | 34 | 17 | 3.570 | 3 |
合计 | 200 | 100 | 21 | 21 |
表2的例子指出,委员的名额增多了,但丙系反而减少一名,令丙系不能接受!
