前提为两条长度相等的线段,假如一条线段两端加上向外的两条斜线,另一条线段两端加上向内的两条斜线,则前者要显得比后者长得多。
培恩洛兹三角形,将三条长方形以不同的视角使其错位地交织在一起,在三条长方体“不合理”(透视)的衔接中,不可思议地创造了一种视觉“扭曲”感,一种强力的视觉穿透力跃然于纸。仔细观察分析这幅图,便可发现我们的视觉被转换了三个角度。按常理应得出三个不同时空的三角图形。然而,把同一时空转移为不同时空并巧妙地整合成一个三角形,一个全然是不可能的三角形,却改变了人们的视觉经验,使“不可能”成了实实在在的可能的视觉图形。
彭罗斯三角(Penrose triangle)是不可能的物体中的一种。最早是由瑞典艺术家Oscar Reutersvärd在1934年製作。英国数学家罗杰·彭罗斯及其父亲也设计及推广此图案,并在1958年2月份的《英国心理学月刊》(British Journal of Psychology)中发表,称之为“最纯粹形式的不可能”。
彭罗斯三角看起来像是一个固体,由三个截面为正方形的长方体所构成,三个长方体组合成为一个三角形,但两长方体之间的夹角似乎又是直角。上述的性质无法在任何一个正常三维空间的物体上实现。这种物件只能存在于一些特定的欧氏三维流形中[1]。
基本介绍
- 中文名:彭罗斯三角形
- 外文名:Penrose triangle
- 别称:不可能三角形
- 提出者:Oscar Reutersvärd
- 套用学科:数学
- 适用领域範围:素描
这种三角形又被称为“不可思议三角形”,是悖理与比例逆反的典型体现。将三条长方形以不同的视觉角度使其错位地交织在一起,在三条长方形“不合理”(透视)的衔接中,不可思议地创造了一种视觉“扭曲”感,一种强力的视觉穿透力跃然于纸上。
< 培恩洛兹三角形 >
它把同一时空转移为不同时空并且巧妙地整合成一个三角形,一个全然悖理的三角形,却改变了人们的视觉经验,使“不可能”成了实实在在的可能的视觉图形。
三角形每一个顶角都产生透视,儘管三个顶角各自体现不同角度的三角形。将三个顶角合成一个整体,就产生一个空间不可能图形。
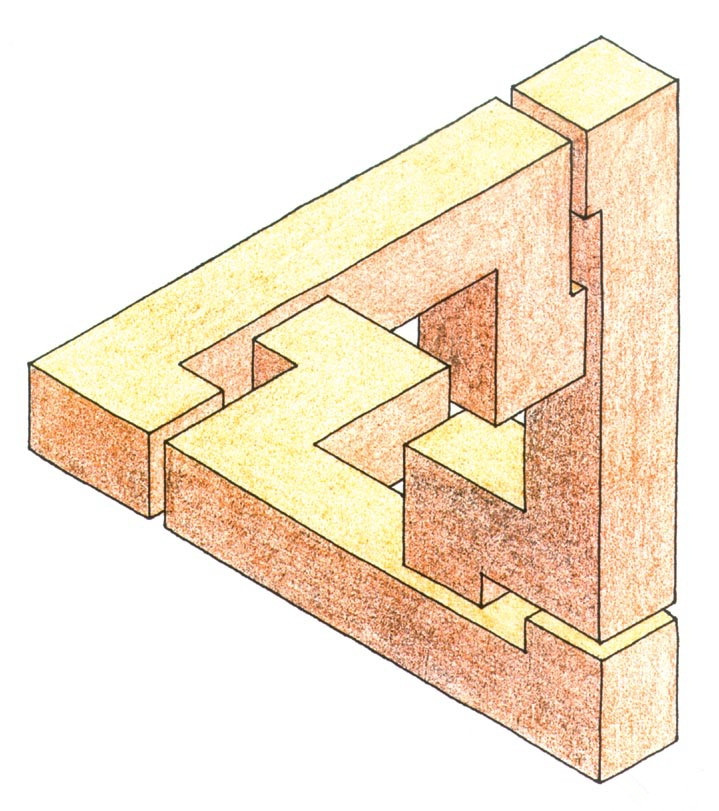
< 路透斯沃德的不可能的三角形 >

