同伦群(homotopy groups)是基本群的高维推广。基本群是从单位闭区间I到拓扑空间X的闭路的同伦等价类和其运算得到的。考虑n维欧氏空间R中的n维方体：

是的边界，即：

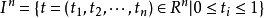
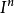
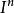
存在i使得，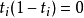

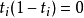
设X为拓扑空间，x₀∈X，用M_n(X，x₀)表示全体连续映射α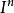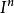：(， )→(X，x₀)所成的集合，α和α′相对于I的同伦关係αα′是M_n(X，x₀)上的一个等价关係，它把M_n(X，x₀)的元素分成一些同伦等价类，用π_n(X，x₀)表示这些等价类所成的集合.定义映射α*β：(I，I)→(X，x₀)，使得：

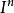
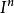
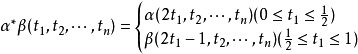
从而，α*β∈M_n(X，x₀)，并且，若α∽α′，β∽β′，则：

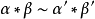
因此，可在π_n(X，x₀)中定义运算：

并且关于这一运算使它构成群，仍记为π_n(X，x₀)，称为拓扑空间X的以x₀为基点的n维同伦群.1维同伦群就是基本群π₁(X，x₀).同伦群还有一种等价定义方式，它是用n维球面S代替n维方体I，这种定义给讨论同伦群的性质有时带来方便.类似基本群的讨论，同伦群具有性质：当拓扑空间是道路连通空间时，其同伦群与基点选取无关;利用连续映射诱导的同伦群之间同态的一些性质得出，同伦群是同伦型不变数(更是拓扑不变的)；当n≥2时，同伦群π_n(X，x₀)是交换群，因而有时把运算写成[α]+[β]。同伦群与同调群的一些基本关係：对于连通复形K的多面体|K|，1维同调群同构于基本群的交换化，即：

这里[π₁(|K|)，π₁(|K|)]表示基本群π₁(|K|)的换位子群。高维同伦群与同调群之间的关係，由赫莱维茨(Hurewicz，W.)的同构定理给出：设|K|是连通复形K的多面体，当n≥2时，若|K|的1，2，…，n-1维同伦群都是平凡群，则π_n(|K|)xH_n(K)。

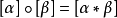
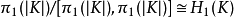
群是一种只有一个运算的、比较简单的代数结构；是可用来建立许多其他代数系统的一种基本结构。

设G为一个非空集合，a、b、c为它的任意元素。如果对G所定义的一种代数运算“·”(称为“乘法”，运算结果称为“乘积”)满足：

(1)封闭性，a·b∈G;

(2)结合律，即(a·b)c = a·(b·c);

(3)对G中任意元素a、b，在G中存在惟一的元素x，y，使得a·x= b，y·a=b，则称G对于所定义的运算“·”构成一个群。例如，所有不等于零的实数，关于通常的乘法构成一个群;时针转动(关于模12加法)，构成一个群。

满足交换律的群，称为交换群。

群是数学最重要的概念之一，已渗透到现代数学的所有分支及其他学科中。凡是涉及对称，就存在群。例如，可以用研究图形在变换群下保持不变的性质，来定义各种几何学，即利用变换群对几何学进行分类。可以说，不了解群，就不可能理解现代数学。

1770年，拉格朗日在讨论代数方程根之间的置换时，首先引入群的概念，而它的名称，是伽罗华在1830年首先提出的。

基本群亦称一维同伦群。对一个拓扑空间联繫一个群的代数结构。在拓扑空间X中对于以同一点x₀为基点的两条闭道路α和β可引入乘法*：

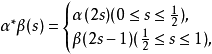
α*β是一条以x₀为基点的闭道路。这种乘法不一定满足结合律，无法引入群结构。但是，在以x₀为基点所有闭路同伦类中，引入乘法：

[α]°[β]=[α*β]，

这种定义是有意义的，并且以x₀为基点的全体闭路同伦类在引入这种乘法后构成一群，称为X的以x₀为基点的基本群，记为π₁(X，x₀).基本群可以不是交换群.对于道路连通空间X，其基本群与基点的选取无关，记为π₁(X).对于两个拓扑空间X与Y之间的连续映射f：(X，p)→(Y，q)，它与X内以p为基点的闭路α的複合映射f°α是Y内以q为基点的闭路，并且两条同伦的闭路与f的複合得出两条同伦的闭路，因此，按照f_*([α])=[f°α]定义映射：

f_*： π₁(X，p)→π₁(Y，q)，

于是f_*为同态，称为f诱导的同态.由此得出基本群是拓扑不变数，进而基本群也是同伦型不变数。

计算基本群常常是将所讨论的空间“归结”或“分解”为更简单的空间以算出其基本群，这些常见的方法有：

1.利用基本群的同伦型不变性.

2.对于乘积空间可利用结论：当X和Y为道路连通空间时，π₁(X×Y)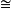π₁(X)×π₁(Y).

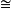
3.利用覆叠空间理论.

4.利用范卡彭定理：若K是连通的复形，K₀，K₁，K₂都是K的连通的子复形，使得

α₀是K₀的一个顶点，i₁和i₂分别是K₀的多面体|K₀|到K₁和K₂的多面体|K₁|和|K₂|的包含映射，则|K|的基本群π₁(|K|，a₀)可从π₁(|K₁|，a₀)与π₁(|K₂|，a₀)的自由乘积中添加关係i_1*(z)=i_2*(z)得到，其中z取遍π₁(|K₀|，a₀)的一切元素。

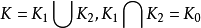
范卡彭定理适用于可剖分空间，并可推广到更一般的加一定限制的拓扑空间。例如，用以上方法可得到圆周S的基本群为π₁(S)Z，可缩空间的基本群为平凡群，默比乌斯(Mo¨bius，A.F.)带M的基本群π₁(M)Z，环面T的基本群为π₁(T)Z×Z，n维球面S(n≥2)的基本群π₁(S)为平凡群，以及克莱因瓶K的基本群π₁(K){t，u|tut=u}(或{a，b|a=b})，这里Z表示整数加群。