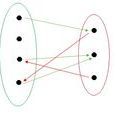
数学上，二元关係用于讨论两个数学对象的联繫。诸如算术中的「大于」及「等于」，几何学中的"相似"，或集合论中的"为...之元素"或"为...之子集"。二元关係有时会简称关係，但一般而言关係不必是二元的。
基本介绍
- 中文名：二元关係
- 外文名：Binary Relation
- 适用範围：数理科学
定义
集合X与集合Y上的二元关係是R=(X,Y,G(R))，其中G(R)，称为R的图，是笛卡儿积X×Y的子集。若 (x,y) ∈G(R) ，则称x是R-关係于y，并记作xRy或R(x,y)。否则称x与y无关係R。但经常地我们把关係与其图等同起来，即：若R⊆X×Y，则R是一个关係。
例如：有四件物件 {球，糖，车，枪} 及四个人 {甲，乙，丙，丁}。 若甲拥有球，乙拥有糖，及丁拥有车，即无人有枪及丙一无所有— 则二元关係"为...拥有"便是R=({球，糖，车，枪}, {甲，乙，丙，丁}, {(球,甲), (糖,乙), (车,丁)})。
其中 R 的首项是物件的集合，次项是人的集合，而末项是由有序对（物件，主人）组成的集合。比如有序对（球，甲）∈G(R)，所以我们可写作"球R甲"，表示球为甲所拥有。
不同的关係可以有相同的图。以下的关係 ({球，糖，车，枪}, {甲，乙，丁}, {(球,甲), (糖,乙), (车,丁)} 中人人皆是物主，所以与R不同，但两者有相同的图。话虽如此，我们很多时候索性把R定义为G(R)， 而 "有序对 (x,y) ∈G(R)" 亦即是 "(x,y) ∈R"。
二元关係可看作成二元函式，这种二元函式把输入元x∈X及y∈Y视为独立变数并求真伪值（即“有序对(x,y) 是或非二元关係中的一元”此一问题）。
若X=Y，则称R为X上的关係。
特殊的二元关係
注：下文我们将採用把二元关係R定义为A × A的子集的做法。
设A是一个集合，则：
空集∅称作A上的空关係（因为∅也是A × A的子集）。
EA = A × A称作A上的全域关係。
IA = {(x,，x)： x∈A} 称作A上的恆等关係。
性质
关係的性质主要有以下五种：自反性，反自反性，对称性，反对称性和传递性。
自反性：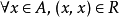
。
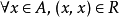
在集合X上的关係R，如对任意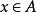
，有
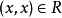，则称R是自反的。
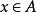
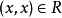
反自反性（自反性的否定的强形式）：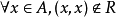
。
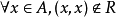
在集合X上的关係R，如对任意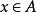 ，有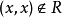
，则称R是反自反的。
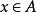
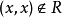
对称性：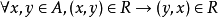
。
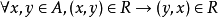
在集合X上的关係R，如果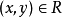有
则必有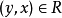
，则称R是对称的。
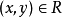
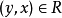
反对称性（不是对称性的否定）：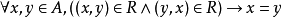
。
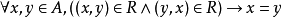
非对称性（对称性的否定的强形式）：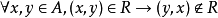
。
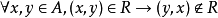
非对称关係是满足反自反性的反对称关係。
传递性：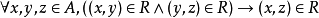
。
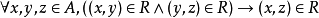
实例
例1：
设A={1,2,3},R1,R2和R3是A上的关係，其中：R1={<1,1>,<2,2>}；R2={<1,1>,<2,2>,<3,3>,<1,2>}；R3={<1,3>}，则R1不是自反的，R3是反自反的，R2是自反的但不是反自反的。
例2：
设A={1,2,3},R1,R2,R3和R4是A上的关係，其中：R1={<1,1>,<2,2>}；R2={<1,1>,<1,2>,<2,1>}；R3={<1,2>,<1,3>}；R4={<1,2>,<2,1>,<1,3>}，则R1既是对称的也是反对称的。R2是对称的但不是反对称的。R3是反对称的但不是对称的。R4既不是对称的也不是反对称的。
例3：
设A={1,2,3}，R1,R2和R3是A上的关係，其中：R1={<1,1>,<2,2>}；R2={<1,2>,<2,3>}；R3={<1,3>}，则R1和R3是A上的传递关係，R2不是A上的传递关係。
关係矩阵
设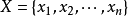
及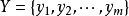
，R是X与Y上的二元关係，令
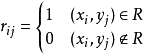，则0,1矩阵
称为R的关係矩阵，记作MR。
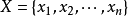
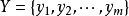
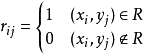
关係图
设R集合A到B上的二元关係，令图G=(V,E)，其中顶点集合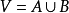
，边集合为E ，且对于任意的
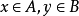，规定
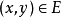若且唯若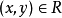
。则称图G是关係R的关係图。
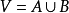
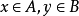
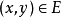
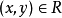
关係的运算
关係的基本运算有以下几种：
设R为二元关係。
R中所有有序对的第一元素构成的集合称为R的定义域，记作dom(R)，即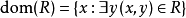
。
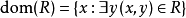
R中所有有序对的第二元素构成的集合称为R的值域，记作ran(R) ，即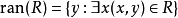
。
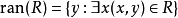
R的定义域和值域的并集称作R的域，记作fld(R)，即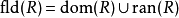
。
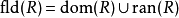
R的逆关係，简称R的逆，记作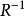
，其中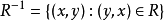
。
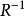
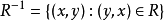
设S也是一个二元关係。R和S的合成记作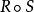
，其定义为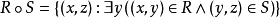
。
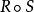
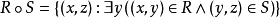
若R是一个集合A上的二元关係，可以在自然数範围内定义R的n次幂。首先规定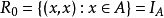
，再递归定义
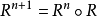。可以证明有
，
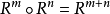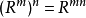成立。
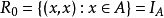
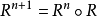
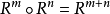
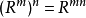
与关係性质的联繫
设R为集合A上的关係，下面给出的六种性质成立的充要条件：
R在A上自反若且唯若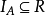
；
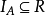
R在A上反自反若且唯若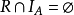
；
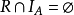
R在A上对称若且唯若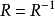
；
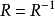
R在A上反对称若且唯若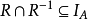
；
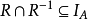
R在A上非对称若且唯若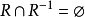
；
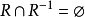
R在A上传递若且唯若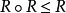
。
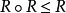
关係的闭包
设R是非空集合A上的关係， R的自反（对称或传递）闭包是A上的关係R' ，满足：
(1) R'是自反的（对称的或传递的）。
(2)
。
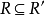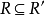
(3) 对A上任何包含R的自反（对称或传递）关係R''有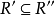
。
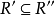
一般将R的自反闭包记作r(R)，对称闭包记作s(R) ，传递闭包记作t(R)。
下列给出了构造闭包的方法：
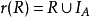
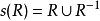
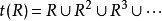
对于有限集合A 上的关係R ，存在一个正整数s，使得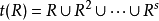
，且s不超过A的元素数。
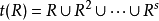
求传递闭包是图论中一个非常重要的问题，例如给定了一个城市的交通地图，可利用求传递闭包的方法获知任意两个地点之间是否有路相连通。可以直接利用关係矩阵相乘来求传递闭包，但那样做複杂度比较高；好一点的办法是在计算矩阵相乘的时候用分治法降低时间複杂度；但最好的方法是利用基于动态规划的Floyd-Warshall算法来求传递闭包。
二元关係的数目
在一个有n个元素的集合（简称n元素集）上，一共有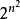
个可能的二元关係。
在n元素集上各种二元关係的数目 | ||||||||
n | 所有 | 传递 | 自反 | 预序 | 偏序 | 全预序 | 全序 | 等价关係 |
0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
1 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 |
2 | 16 | 13 | 4 | 4 | 3 | 3 | 2 | 2 |
3 | 512 | 171 | 64 | 29 | 19 | 13 | 6 | 5 |
4 | 65536 | 3994 | 4096 | 355 | 219 | 75 | 24 | 15 |
OEIS | A002416 | A006905 | A053763 | A000798 | A001035 | A000670 | A000142 | A000110 |
注：
- 反自反关係和自反关係的数目一样多。
- 严格偏序（反自反的传递关係）的数目和偏序的一样多。
- 全序即是那些同时是全预序的偏序。透过容斥原理的想法，可知那些既不是偏序也不是全预序的预序数目是：预序的数目，减去偏序的数目，再减去全预序的数目，最后加上全序的数目，即0, 0, 0, 3, 85, ...
- 等价关係的数目是集合划分的数目，即贝尔数。
各个二元关係之间可组成二元组（某关係及其补集），除了在n=0时，空关係的补集即其自身。那些不符合对称性的二元关係也可组成四元组（某关係、补集、逆、逆的补集）。