空关係是一种特殊关係，指关係集A×B中的子集∅。非空集合中的空关係是反自反的、对称的、反对称的和传递的，但不是自反的；空集合中的空关係则是自反的、反自反的、对称的、反对称的和传递的。非空集合的空关係的矩阵各元素都是0。
基本介绍
- 中文名：空关係
- 外文名： empty relation
- 所属学科：离散数学
- 符号表示：∅
- 相关概念：二元关係、全关係、反自反性等
定义
定义1 设A，B是两个集合，R是A×B的任意一个子集，即
若
称R为空关係。
若
称为全关係。
当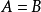
时，称二元关係
为A上的二元关係。
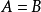
当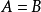时，记
称之为A上的恆等关係。
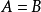
空关係是一种特殊关係，指关係集A×B中的子集∅。非空集合中的空关係是反自反的、对称的、反对称的和传递的，但不是自反的；空集合中的空关係则是自反的、反自反的、对称的、反对称的和传递的。非空集合的空关係的矩阵各元素都是0。
定义2 集合A上的关係是从A到A的关係。
集合A到它自身的关係是特别令人感兴趣的。
通常集合A上不同关係的数目依赖于A的基数。如果|A|=n,那幺|A×A|=n2，可知A 上关係的子集有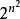
个，因为一个子集代表一个A 上的关係，所以A 上的关係有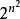个不同的二元关係。
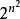
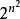
例如
，则在A上可以定义
个不同的关係。当然，大部分的关係没有什幺实际意义，但是,对于任意集合A都有3种特殊的关係，它们是:
定义3 称
为A上的空关係，称
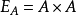为A上的全关係，称
为A上的相等关係(或恆等关係)。
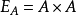
例题解析
例1 设
R是P(A)上的包含关係，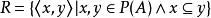
则
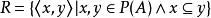
有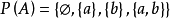
。
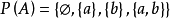
例2 给定一个非空集合A，试讨论集合A上的全域关係A×A以及空关係
的性质。
解：(1)全域关係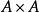
显然有自反性、对称性和传递性，但显然没有反自反性。
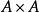
至于反对称性，要看集合A的元素个数而定。
情形一：如果
那幺显然它上面的全域关係有反对称性。
情形二：如果
，那幺显然它上面的全域关係没有反对称性。
(2) 因为A是非空集合，所以容易验证A上的空关係有对称性、传递性、反自反性、反对称性，但没有自反性。
二元关係的性质
设R是集合A上的一个二元关係，即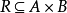
，于是
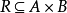
(1)若对于
，满足
则称关係R有自反性，或称R是A上的自反关係。
(2)若对于，满足
则称关係R有反自反性，或称R是A上的反自反关係。
(3)若对于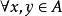
，满足当
有
则称关係R有对称性。或称R是A上的对称关係。
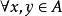
(4)若对于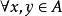，满足当
且有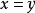
，则称关係R有反对称性，或称R是A上的反对称关係。
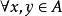
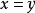
(5)若对于
，满足当
且
时，有
则称关係R有传递性，或称R是A上的传递关係。
注：1. 有自反性的关係一定没有反自反性，有反自反性的关係也一定没有自反性，这说明自反性与反自反性不可能共存于同一个关係之中。但是有这样的关係存在，它既不是自反的，也不是反自反的。
2. 对称性和反对称性有可能共存于同一个关係之中。同时也存在这样的关係，它既不是对称的，也不是反对称的。