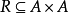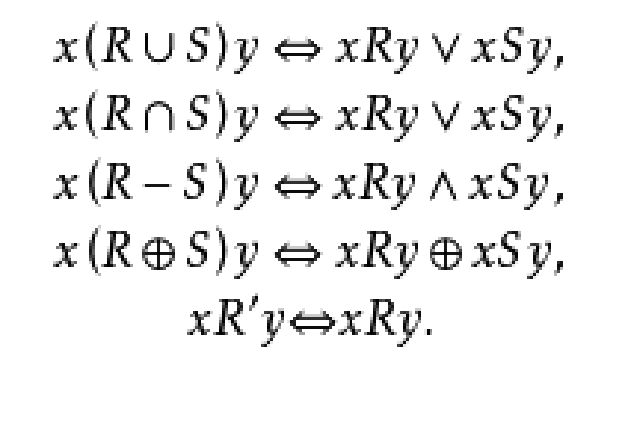关係常指二元关係,数学的基本概念之一,关係是在集合的基础上定义的一个重要的概念,与集合的概念一样,关係的概念在计算机科学中也是最基本的。它主要反映元素之间的联繫和性质,在计算机科学中有重要的意义,如有限自动机和形式语言、编译程式设计、信息检索、数据结构以及算法分析和程式设计的描述中经常出现。
基本介绍
- 中文名:关係
- 外文名:binary relation、relation
- 别名:二元关係
- 所属学科:数学
- 用途:反映元素之间的联繫和性质
基本概念
定义
给定任意集合A和B,若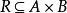 ,则称R为从A到B的二元关係,特别在A=B时,称R为A上的二元关係.可见,R是有序对的集合.若
,则称R为从A到B的二元关係,特别在A=B时,称R为A上的二元关係.可见,R是有序对的集合.若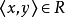 ,则也表示为
,则也表示为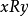 ,即
,即
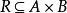
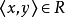
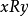
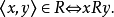
若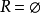 ,则称R为A到B上空关係;若R=A×B,称R为A到B上全域关係.特别当A=B时,称
,则称R为A到B上空关係;若R=A×B,称R为A到B上全域关係.特别当A=B时,称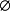 为A上空关係,称R=AXA为A上的全域关係.称
为A上空关係,称R=AXA为A上的全域关係.称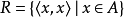 为A上的恆等关係,记为
为A上的恆等关係,记为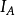 .
.
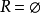
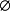
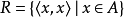
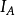
定义域、值域和域
令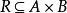 ,且
,且
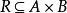
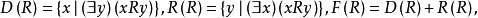
显然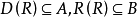 。
。
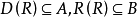
关係是有序对的集合,对它可进行集合运算,其结果也是有序对的集合,即也是某一种二元关係。令R和S是两个二元关係,则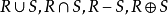 和R'都分别定义了某一种二元关係,并且可表示成:
和R'都分别定义了某一种二元关係,并且可表示成:
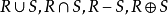
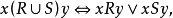
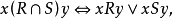
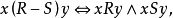
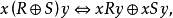
关係矩阵与关係图
表达从有穷集合到有穷集合的二元关係时,矩阵和有向图都是得力的工具。
定义 给集合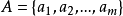 和
和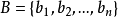 ,且
,且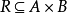 .若
.若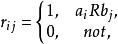 则称矩阵
则称矩阵 为R的关係矩阵。
为R的关係矩阵。
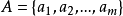
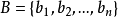
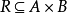
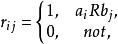

当给定关係R,可求出关係矩阵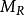 ;反之,若给出关係矩阵
;反之,若给出关係矩阵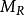 ,也能求出关係R。
,也能求出关係R。
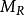
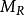
集合A上的二元关係R也可用有向图表示.具体方法是:用小圆圈表示A中的元素,小圆圈称为图的结点,把对应于元素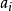 和
和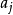 的结点分别标记
的结点分别标记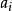 和
和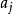 若
若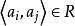 ,则用弧线段或直线段把
,则用弧线段或直线段把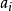 和
和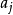 连线起来,并在弧线或直线上设定一箭头,使之由
连线起来,并在弧线或直线上设定一箭头,使之由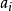 指向
指向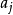 ;若
;若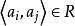 ,则在结点
,则在结点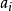 上画一条带箭头的自封闭曲线或有向环,称这样的弧线或封闭曲线为弧或有向环,这样得到的有向图
上画一条带箭头的自封闭曲线或有向环,称这样的弧线或封闭曲线为弧或有向环,这样得到的有向图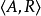 叫做关係R的图示,简称关係图,记为
叫做关係R的图示,简称关係图,记为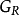 。
。
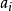
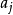
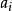
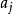
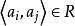
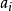
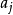
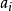
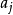
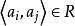
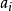
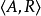
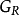
关係的性质
关係的性质是指集合中二元关係的性质,这些性质扮演着重要角色,下面将定义这些性质。并给出它的关係矩阵和关係图的特点。
自反 令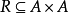 ,若对A中每个x,都有
,若对A中每个x,都有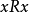 ,则称R是自反的,即A上关係R是自反的
,则称R是自反的,即A上关係R是自反的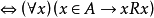 。
。
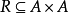
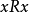
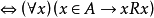
在全集U中所有子集的集合中,包含关係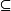 是自反的,相等关係=也是自反的;但是,真包含关係
是自反的,相等关係=也是自反的;但是,真包含关係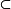 不是自反的,整数集合Z中,关係≤是自反的,而关係<不是自反的。
不是自反的,整数集合Z中,关係≤是自反的,而关係<不是自反的。
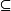
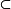
反自反 令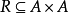 ,若对于A中每个x,有
,若对于A中每个x,有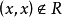 ,则称R是反自反的,即A上关係R是反自反的。
,则称R是反自反的,即A上关係R是反自反的。
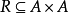
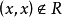
该定义表明了,一个反自反的关係R中,不应包括有任何相同元素的有序对,由定义说明中可知真包含关係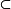 是反自反的,但包含关係
是反自反的,但包含关係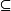 不是反自反的;小于关係<是反自反的,而≤不是反自反的。
不是反自反的;小于关係<是反自反的,而≤不是反自反的。
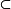
应该指出,任何一个不是自反的关係,未必是反自反的;反之,任何一个不是反自反的关係,未必是自反的,这就是说,存在既不是自反的也不是反自反的二元关係。
对称 令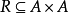 ,对于A中每个x和y,若xRy,则yRx,称R是对称的,即A上关係R是对称的
,对于A中每个x和y,若xRy,则yRx,称R是对称的,即A上关係R是对称的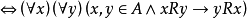 。
。
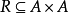
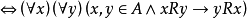
该定义表明了,在表示对称的关係R的有序对集合中,若有有序对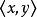 ,则必定还会有有序对
,则必定还会有有序对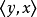 。
。
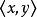
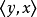
在全集U的所有子集的集合中,相等关係是对称的,包含关係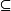 和真包含关係
和真包含关係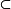 都不是对称的;在整数集合Z中,相等关係=是对称的,而关係≤和<都不是对称的。
都不是对称的;在整数集合Z中,相等关係=是对称的,而关係≤和<都不是对称的。
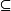
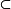
反对称 令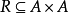 ,对于A中每个x和y,若xRy且yRx,则x=y,称R是反对称的,即A上关係R是反对称的
,对于A中每个x和y,若xRy且yRx,则x=y,称R是反对称的,即A上关係R是反对称的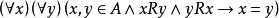 。
。
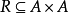
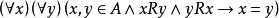
该定义表明了,在表示反对称关係R的有序对集合中,若存在有序对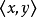 和
和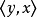 ,则必定是x=y,或者说,在R中若有有序对
,则必定是x=y,或者说,在R中若有有序对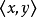 ,则除非x=y,否则必定不会出现
,则除非x=y,否则必定不会出现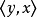 。
。
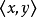
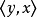
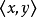
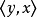
在全集U的所有子集的集合中,相等关係=,包含关係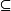 和真包含关係
和真包含关係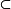 都是反对称的,但全域关係不是反对称的.在整数集合Z中,=,≤和<也都是反对称的。
都是反对称的,但全域关係不是反对称的.在整数集合Z中,=,≤和<也都是反对称的。
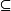
可见,有些关係既是对称的,又是反对称的,如相等关係;有些关係是对称的,但不是反对称的,如Z中的“绝对值相等”;有些关係是反对称的,但不是对称的,如Z中的≤和<;还有的关係既不是对称的,又不是反对称的,例如,A={a,c,b}中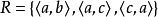 .
.
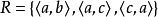
传递 令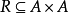 ,对于A中每个x,y,z,若xRy且yRx,则xRz,称R是传递的,即A上关係R是传递的
,对于A中每个x,y,z,若xRy且yRx,则xRz,称R是传递的,即A上关係R是传递的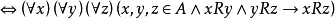
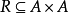
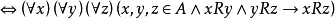
该定义表明了,在表示可传递关係R的有序对集合中,若有有序对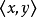 和
和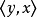 ,则必有有序对
,则必有有序对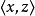 。
。
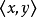
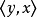
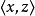
显然,上述提到的关係中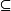 ,
,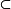 ,=和≤,<,=都是传递的,在直线的集合中,平行关係是传递的,但垂直关係不是传递的。
,=和≤,<,=都是传递的,在直线的集合中,平行关係是传递的,但垂直关係不是传递的。
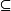
通过上面几个实例,看出:
①若A上关係R是自反的,则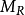 中主对角线上元素全为1,而
中主对角线上元素全为1,而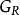 中每个结点有有向环;反之亦然;
中每个结点有有向环;反之亦然;
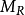
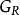
②若A上关係R是反自反的,则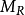 中主对角线上元素全为0,而
中主对角线上元素全为0,而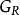 中每个结点无有向环;反之亦然;
中每个结点无有向环;反之亦然;
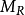
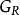
③若A上关係R是对称的,则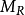 是对称矩阵,而
是对称矩阵,而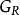 中任何两结点若有弧,弧必成对出现;反之亦然;
中任何两结点若有弧,弧必成对出现;反之亦然;
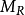
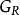
④若A上关係R是反对称的,则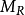 中主对角线元素不能同时为1,而
中主对角线元素不能同时为1,而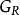 中若两结点间有弧,弧不能成对出现;反之亦然;
中若两结点间有弧,弧不能成对出现;反之亦然;
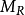
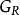
⑤若A上关係R是传递的,则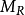 中若
中若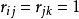 ,则
,则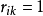 ,而
,而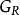 中若有弧
中若有弧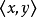 和
和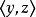 ,则必有弧
,则必有弧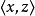 ;反之亦然。
;反之亦然。
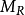
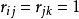
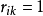
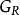
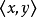
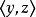
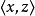
此外,还有:
①任何集合上的相等关係=是自反的,对称的、反对称的和传递的,但不是反自反的。
②整数集合Z中,关係≤是自反的、反对称的和传递的,但不是反自反的和对称的,关係<是反自反的、反对称的和传递的,但不是自反的和对称的。
③非空集合上的空关係是反自反的、对称的、反对称的和传递的,但不是自反的,空集合上的空关係则是自反的、反自反的、对称的、反对称的和传递的。
④非空集合上的全域关係是自反的、对称的和传递的,但不是反自反的和反对称的。
定理 设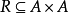 ,若R是反自反的和传递的,则R是反对称的。
,若R是反自反的和传递的,则R是反对称的。