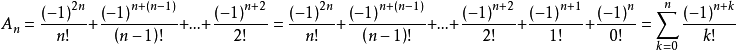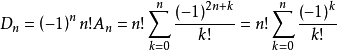表述为：编号是1、2、…、n的n封信，装入编号为1、2、…、n的n个信封，要求每封信和信封的编号不同，问有多少种装法？
对这类问题有个固定的递推公式，记n封信的错位重排数为Dn，则D1=0，D2=1，
Dn=（n-1）（Dn-2+Dn-1） 此处n-2、n-1为下标。

n>2

我们只需记住Dn的前几项：D1=0，D2=1，D3=2，D4=9，D5=44。我们只需要记住结论，进行计算就可以。

【例】五个盒子都贴了标籤，全部贴错的可能性有多少种？

即全贴错标籤，N个项数全部排错的可能数，可以总结出数列：

0，1，2，9，44，265，………

可以得到这样一个递推公式：（N-1）*（A+B）=C （A是第一项，B是第二项，C是第三项，N是项数）

s(n)=(n-1) [ s（n-1）+s（n-2）]

s(2)=1,s(3)=2

s(4)=3*(1+2)=9

s(5)=4*(2+9)=44

s(6)=5*(9+44)=265 ....................

公式由来 把编号 1-------------n的小球放到编号1------n的盒子里，全错位排列（1号球不在1号盒，2号球不在2号盒，依次类推），共有几种情况？

------------------------------------------------------

设n个球全放错的情况有 s（n）种

1号盒子可以选[2,n] 共（n-1）种选择，设1号盒选择某号球后对应的错排次数是 a

（n-1）个选择对应的错排次数是相同的 ，则 s（n）=（n-1）a

不妨设1号盒选择2号球

1： 2号盒选择1号球，剩下 （n-2）个球去错排，有 s（n-2）种情况

2： 2号盒不选择1号球，则后面总有一个盒子选择1号球，我们可以把1号球和2号球在放入盒子前互换位置，

对问题没有影响，此时就相当于对（n-1）个球去错排，有s（n-1）种情况

于是a= s（n-1)+s(n-2)

s(n)=(n-1) [ s（n-1）+s（n-2）]

s(2)=1,s(3)=2

s(4)=3*(1+2)=9

s(5)=4*(2+9)=44

s(6)=5*(9+44)=265 ....................

【例题】四位厨师聚餐时各做了一道拿手菜。现在要求每人去品尝一道菜，但不能尝自己做的那道菜。问共有几种不同的尝法？
A．6种 B．9种 C．12种 D．15种

根据4位厨师的错位重排数D4=9，所以由公式可以看出是有9种。

已经D1=0，D2=1，Dn=（n-1）（Dn-2+Dn-1），求Dn。

Dn = (n-1)Dn-1 + (n-1)Dn-2

Dn-nDn-1 = -[Dn-1 - (n-1)Dn-2]=(-1)^2*[Dn-2 - (n-2)Dn-3]=...(-1)^(n-2)*(D2-2D1)

设Dn-nDn-1=Cn

Cn=(-1)^(n-2)*1=(-1)^n

则 Dn = (-1)^n + nDn-1

两边同除(-1)^n

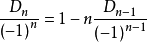
设Dn/(-1)^n=Bn

Bn = 1 - nBn-1

两边同除n!

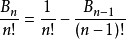
设Bn/n!=An

An+An-1=1/n!..................(1)

An-1+An-2=1/(n-1)!.........(2)

............

A2+A1=1/2!......................(n-1)

A1+D1=0..........................(n)

(1)-(2)+(3)..............(n)得