没有变元(或变元被其定义域的元素普遍赋值后)的原子公式,即基础原子公式,简称“基原子”。原子公式以及它的否定形式都是文字。不包含变元(或变元被其定义域的元素普遍赋值后) 的文字即基础文字(基文字)。文字以及它们的析取,都称为子句,由子句构成的集合即子句集。
基本介绍
- 中文名:子句集
- 外文名:set of clauses
- 所属学科:数学
- 简介:由子句构成的集合
- 相关概念:子句,文字,基子句等
定义
不含有任何连线词的谓词公式叫原子公式,简称原子,而原子或原子的否定统称文字。子句就是由一些文字组成的析取式。由子句构成的集合称为子句集。将没有变元出现的子句集分别称作基子句集。
例如,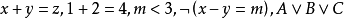 都是子句。用
都是子句。用 表示空子句,即不包含任何文字的子句。
表示空子句,即不包含任何文字的子句。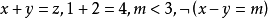 构成一个子句集S:
构成一个子句集S: 。相反,以下命题表达式不是单独的子句:
。相反,以下命题表达式不是单独的子句: 。因为它们的最外层都是
。因为它们的最外层都是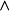 连线的,因此前者可以化为A 和B 两个子句,后者可以化为
连线的,因此前者可以化为A 和B 两个子句,后者可以化为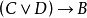 和C两个子句。不能区分在子句集中的子句是独立的命题,还是一个合取範式(由
和C两个子句。不能区分在子句集中的子句是独立的命题,还是一个合取範式(由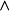 连线的表达式)。在本例中,命题
连线的表达式)。在本例中,命题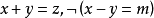 和命题
和命题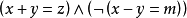 的子句集都是
的子句集都是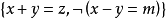 。
。
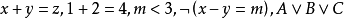

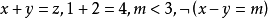


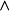
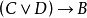
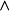
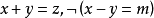
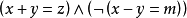
相关概念
定义1不含有任何连线词的谓词公式叫原子公式,简称原子,而原子或原子的否定统称文字。
定义2子句就是由一些文字组成的析取式。
定义3不包含任何文字的子句称为空子句,记为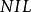 。
。
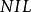
定义4由子句构成的集合称为子句集。
定义5设谓词公式G的子句集为S,则按下述方法构造的个体变元域H称为公式G或子句集S的Herbrand域,简称H域。
(1)令H0是S中所出现的常量的集合。若S中没有常量出现,就任取一个常量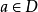 ,规定
,规定 。
。
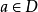

(2)令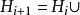 {S中所有的形如
{S中所有的形如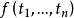 的元素),其中
的元素),其中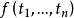 是出现于
是出现于
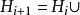
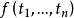
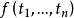
G中的任一函式符号,而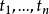 是
是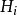 中的元素。i=0,1,2,…。
中的元素。i=0,1,2,…。
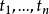
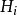
定义6下列集合称为子句集S的原子集:
A={所有形如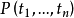 的元素}
的元素}
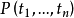
其中,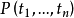 是出现在S中的任一谓词符号,而
是出现在S中的任一谓词符号,而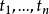 则是S的H域上的任意元素。
则是S的H域上的任意元素。
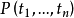
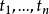
定义7将没有变元出现的原子、文字、子句和子句集分别称作基原子、基文字、基子句和基子句集。
定义8当子句集S中的某个子句C中的所有变元符号均以其H域中的元素替换时,所得到的基子句称作C的一个基例。
定义9(可满足性、不可满足性)对于一个变元自由的一阶语言公式G,如果至少存在一个D论域上的一个解释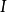 ,在此解释下G为真,则称G是可满足的,即
,在此解释下G为真,则称G是可满足的,即 ;反之,如果对于任何解释G均为假,则称G是不可满足的,即
;反之,如果对于任何解释G均为假,则称G是不可满足的,即 。
。
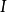


对于一个变元自由的一阶语言公式集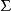 ,即
,即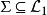 ,如果至少存在一个D的解释
,如果至少存在一个D的解释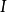 ,在此解释下,
,在此解释下,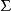 的每个以D为论域的公式均为真,则称
的每个以D为论域的公式均为真,则称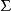 为可满足的;如果D的所有解释
为可满足的;如果D的所有解释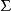 都有假公式,则称
都有假公式,则称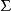 是不可满足的。
是不可满足的。
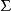
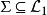
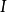
不可满足意义下的一致性
定理1设有谓词公式G,而其相应的子句集为S,则G是不可满足的充分必要条件是S是不可满足的。
要再次强调:公式G与其子句集S并不等值,只是在不可满足意义下等价。
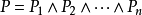
当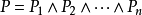 时,若设P的子句集为
时,若设P的子句集为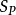 ,
,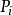 的子句集为
的子句集为 ,则一般
,则一般
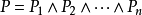
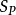
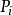

情况下,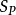 并不等于
并不等于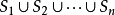 ,而是要比
,而是要比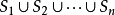 複杂得多。但是,在不可满足的意义下,子句集
複杂得多。但是,在不可满足的意义下,子句集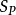 与
与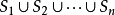 是一致的,即
是一致的,即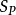 不可满足
不可满足
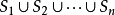 不可满足。
不可满足。
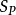
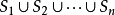
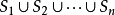
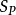
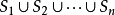
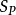

海伯伦理论
H域上的解释
定义10如果子句集S的原子集为A,则对A中各元素的真假值的一个具体设定都是S的一个H解释。
可以证明,在给定域D上的任一个解释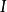 ,总能在H域上构造一个解释
,总能在H域上构造一个解释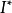 与之对应,使得如果D域上的解释能满足子句集S,则在H域的解释
与之对应,使得如果D域上的解释能满足子句集S,则在H域的解释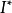 也能满足S(即若
也能满足S(即若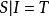 ,就有
,就有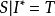 )。
)。
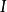
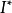
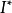
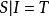
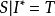
定理2设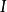 是子句集S在域D上的一个解释,则存在对应于
是子句集S在域D上的一个解释,则存在对应于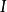 的H域解释
的H域解释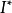 ,使得若有
,使得若有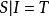 ,就必有
,就必有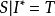 。
。
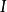
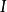
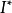
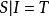
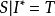
定理3子句集S不可满足的充要条件是S对H域上的一切解释都为假。
证明:充分性:若S在一般域D上是不可满足的,必然在H域上是不可满足的,从而对H域上的一切解释都为假。
必要性:若S在任一H解释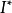 下均为假,必然会使S在D域上的每一个解释为假。否则,如果存在一个解释
下均为假,必然会使S在D域上的每一个解释为假。否则,如果存在一个解释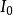 使S为真,那幺依据定理2可知,一定可以在H域找到相对应的一个解释
使S为真,那幺依据定理2可知,一定可以在H域找到相对应的一个解释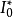 使S为真。这与S在所有H解释下均为假矛盾。
使S为真。这与S在所有H解释下均为假矛盾。
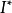
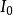
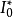
定理4子句集S不可满足的充要条件是存在一个有限的不可满足的基例集S’。
该常理称为Herbrand定理。

