在公元前1650年左右的莱因德数学纸草书中，稜锥已经作为数学对象被几何学家研究。纸草书的56至59题是有关正方锥的底边、高以及底面和侧面形成的二面角之间关係的计算，如已知高和底边长度，求二面角等。传说由欧几里德在公元前三世纪写成的《几何原本》中，第十二章第七个命题证明了：三角柱的体积等于同底同高的三角锥的三倍，但《几何原本》中没有给出直接的稜锥体积公式。公元一世纪左右成书的《九章算术》第五章中的第十二题，计算了正方锥、直方锥（阳马）、直三角锥（鳖臑）的体积，并给出了通用公式。公元三世纪中叶，数学家刘徽在给《九章算术》作的注中，运用极限思想证明了稜锥的体积公式。

稜锥的底面: 稜锥中的多边形叫做稜锥的底面。

稜锥的侧面: 稜锥中除底面以外的各个面都叫做稜锥的侧面。。

稜锥的侧棱: 相邻侧面的公共边叫做稜锥的侧棱。

稜锥的顶点; 稜锥中各个侧面的公共顶点叫做稜锥的顶点。

稜锥的高: 稜锥的顶点到底面的距离叫做稜锥的高。

稜锥的对角面; 稜锥中过不相邻的两条侧棱的截面叫做对角面。

稜锥是多面体中重要的一种，它有两个本质特徵：

①有一个面是多边形；

②其余的各面是有一个公共顶点的三角形，二者缺一不可。

因此稜锥有一个面是多边形，其余各面都是三角形。但是也要注意“有一个面是多边形，其余各面都是三角形”的几何体未必是稜锥。

稜锥的底面可以是三角形、四边形、五边形……我们把这样的稜锥分别叫做三稜锥、四稜锥、五稜锥……

如果一个稜锥的底面是正多边形，且顶点在底面的射影是底面的中心，这样的稜锥叫做正稜锥。

正稜锥的各侧棱都相等，各侧面都是全等的等腰三角形。

正稜锥的斜高：正稜锥侧面等腰三角形底边上的高，叫做正稜锥的斜高。

定理：如果稜锥被平行于底面的平面所截，那幺所得的截面与底面相似，截面面积与底面面积的比等于顶点到截面距离与稜锥高的平方比。

推论1：如果稜锥被平行于底面的平面所截，则稜锥的侧棱和高被截面分成的线段比相等。

推论2：如果稜锥被平行于底面的平面所截，则截得的小稜锥与原稜锥的侧面积之比也等于它们对应高的平方比，或它们的底面积之比。

侧棱长都相等的稜锥，它的顶点在底面内的射影是底面多边形的外接圆的圆心（外心），同时侧棱与底面所成的角都相等。

侧面与底面的交角都相等的稜锥，它的二面角都是锐二面角，所以顶点在底面内的射影在底多边形的内部，并且它到各边的距离相等即为底多边形的内切圆的圆心（内心），且各侧面上的斜高相等。如果侧面与底面所成角为α，则有S底=S侧cosα。如图画出了射影是外心和内心的情况。

稜锥的侧面积及全面积

稜锥的侧面展开图是由各个侧面组成的，展开图的面积，就是稜锥的侧面积，则

S稜锥侧=S1+S2+…+Sn（其中Si，i=1，2…n为第i个侧面的面积）

S全=S稜锥侧+S底

稜锥的底面积公式:S底=长×宽

稜锥和圆锥统称锥体，锥体的体积公式是： v=1/3sh（s为锥体的底面积，h为锥体的高）。

斜稜锥的侧面积=各侧的面积之和

正稜锥的侧面积：S正稜锥侧=1/2chˊ（c为底面周长，hˊ为斜高）。

稜锥的中截面面积：S中截面=1/4S底面

正稜锥各侧棱相等，各侧面都是全等的等腰三角形，各等腰三角形底边上的高相等（它叫做正稜锥的斜高）；

正稜锥的高、斜高和斜高在底面内的射影组成一个直角三角形，正稜锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形。

正稜锥的侧棱与底面所成的角都相等；正稜锥的侧面与底面所成的二面角都相等。

正稜锥的侧面积：如果正稜锥的底面周长为c，斜高为h’，那幺它的侧面积是 s=1/2ch

正稜锥的直观图由底面和顶点所决定。正稜锥底面的画法与直稜柱底面的画法相同。顶点和底面中心的距离等于它的高。下面以正五稜锥为例，说明正稜锥的直观图的画法。

画一个底面边长为5 cm，高为11.5 cm的正五稜锥的直观图，比例尺是 。

画法：

（1）画轴。画x′轴、y′轴、z′轴，记坐标原点为O′，使∠x′O′y′=45°（或135°），∠x′O′z′=90°。如图（1）

（2）画底面。按x′轴、y′轴画正五边形的直观图ABCDE，按比例尺取边长等于5÷5=1（cm），并使正五边形的中心对应于点O′。

（3）画高线。在z′轴取O′S=11.5÷5=2.3（cm）。

（4）成图。连结SA、SB、SC、SD、SE，并加以整理（去掉辅助线，将被遮挡的部分改为虚线），就得到所画的正五稜锥的直观图。

稜锥的底面和平行于底面的一个截面间的部分，叫做稜台。由三稜锥，四稜锥，五稜锥……截得的稜台，分别叫做三稜台，四稜台，五稜台……

由正稜锥截得的稜台叫做正稜台。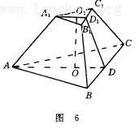

三稜台

正稜台的性质：

（1）正稜台的侧棱相等，侧面是全等的等腰梯形。各等腰梯形的高相等，它叫做正稜台的斜高；（2）正稜台的两底面以及平行于底面的截面是相似正多边形；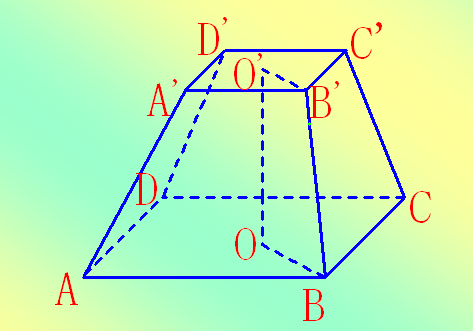

四稜台

（3）正稜台的两底面中心连线、相应的边心距和斜高组成一个直角梯形；两底面中心连线、侧棱和两底面相应的半径也组成一个直角梯形。

两个平行的面分别叫做上底面和下底面，其余的面叫做侧面，侧面相交的线段叫做侧棱，3条侧棱相交的点叫做顶点。

正稜台各侧面的高叫做稜台的斜高。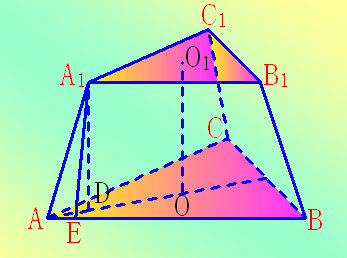

三稜台2

稜台的体积公式:V=[S+S'+(SS')^1/2]h/3

任意平面截稜锥所得截面均为多边型形，不为圆面。